TREES STRUCTURE

Fred Agbo

2025-10-29

Announcements

  • Welcome!
  • We will introduce one of the hierarchical collections - Trees
    • Readings:
      • FDS - Lambert: Chapter 10
      • DS&A - John et al.: Chapter 8, 9
  • Problem set 4 is posted and due next week Monday November 3

Learning Objectives

  • Describe the features of a tree
  • Describe various types of tree traversals
  • Recognize three common applications where it is appropriate to use a tree
  • Describe the features of a binary search tree and the operations on it
  • Recognize the three common applications where it is appropriate to use a binary search tree
  • Describe the features of an expression tree and the operations on it
  • Use an expression tree in recursive descent parsing
  • Describe the features of a heap and the operations on it
  • Provide a complexity analysis of the heap sort

An Overview of Trees

  • A tree is a hierarchical data structure consisting of items called nodes, with a single node designated as the root.
  • Ideas of predecessor and successor are replaced with parent and child
  • Each node may have zero or more child nodes.
  • There are no cycles; each child has exactly one parent (except the root, which has none).

Tree Terminology

  • Summary of terms Used to describe Trees
Term Definition
Node An item stored in a tree
Root The topmost node in a tree (only node without a parent)
Child A node immediately below and directly connected to a given node
Parent A node immediately above and directly connected to a given node
Siblings The children of a common parent
Leaf A node that has no children
Interior node A node that has at least one child
Edge/Branch/Link The line that connects a parent to its child

Tree Terminology (cont.)

  • Summary of terms Used to describe Trees
Term Definition
Descendant A node’s children, its children’s children, and so on
Ancestor A node’s parent, its parent’s parent, and so on
Path The sequence of edges that connect a node and one of its descendants
Path length The number of edges in a path
Depth or level Equals the length of the path connecting it to the root
Height The length of the longest path in the tree
Subtree The tree formed by considering a node and all its descendants

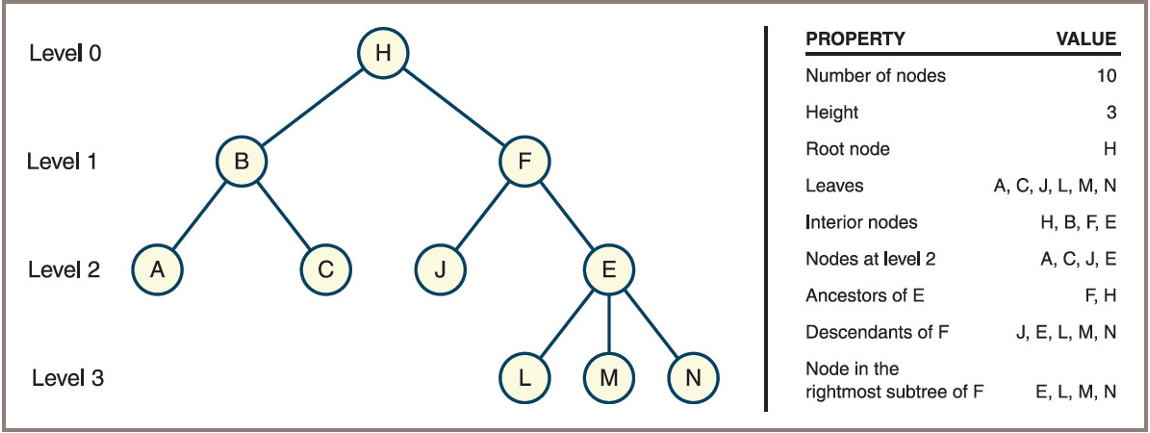
Tree Terminology (example)

General Trees and Binary Trees

  • General tree
    • Above is an example of a general Tree
  • Binary tree
    • Each node has at most two children
    • Children are referred to as the left child and the right child

General Trees and Binary Trees

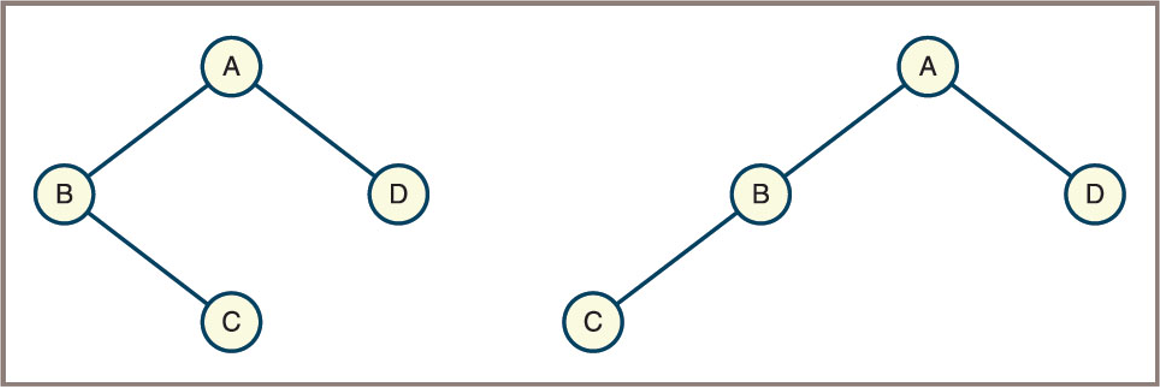
  • Two unequal binary trees that have the same sets of nodes shown here
    • Are not the same when they are considered binary trees
    • Are the same when they are considered general trees

Recursive Definitions of Trees

  • General tree
    A general tree is either empty or consists of a finite set of nodes \(T\).
    • One node \(r\) is distinguished from all others and is called the root.
    • The set \(T - \{r\}\) is partitioned into disjoint subsets, each of which is itself a general tree.
  • Binary tree
    A binary tree is either empty or consists of a root plus a left subtree and a right subtree, each of which is a binary tree.

Check!

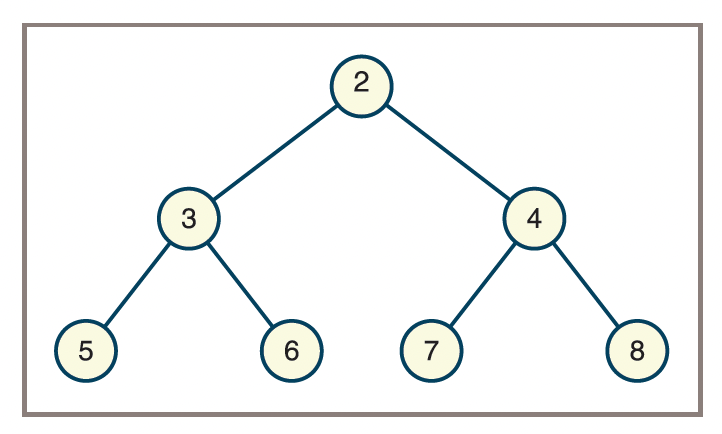
  • From the tree above:
    • What are the leaf nodes in the tree?
    • What are the interior nodes in the tree?
    • What are the siblings of node 7?
    • What is the height of the tree?
    • How many nodes are in level 2?
    • Is the tree a general tree, a binary tree, or both?

Why Use a Tree?

  • Trees nicely represent hierarchical structures
  • Parse tree
    • Describes the syntactic structure of a sentence in terms of its components
    • Such as noun phrases and verb phrases
    • See Figure on the next slide
  • File system structures are also tree-like

Why Use a Tree: Parse Tree

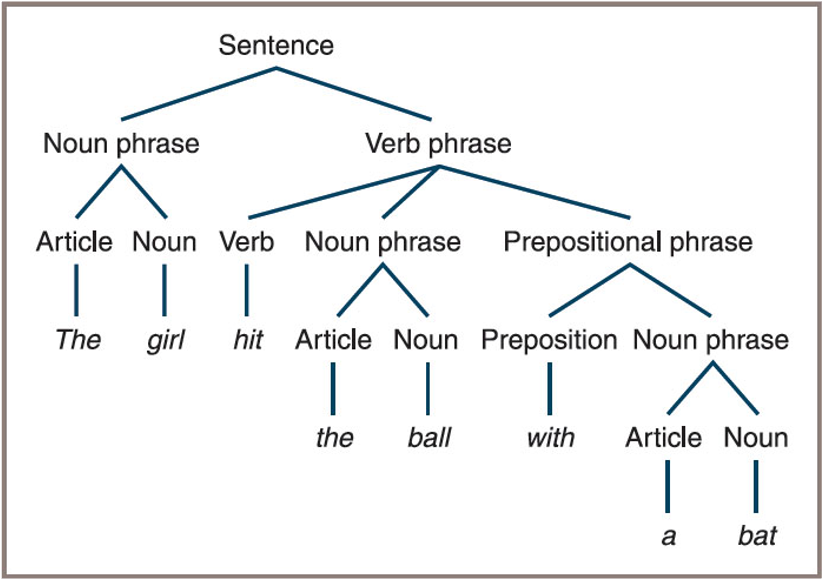
  • A parse tree for a sentence The girl hit the ball with a bat

Why Use a Tree: File System

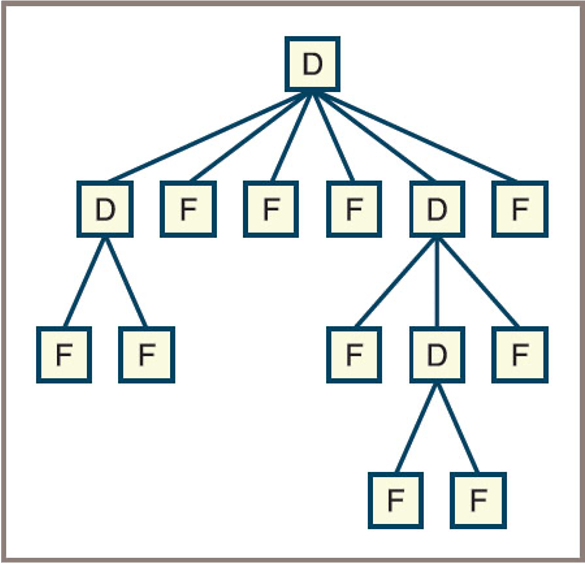
  • A file system structure indicating D as directory (now folder) and F as file

Why Use a Tree: Binary Sorted

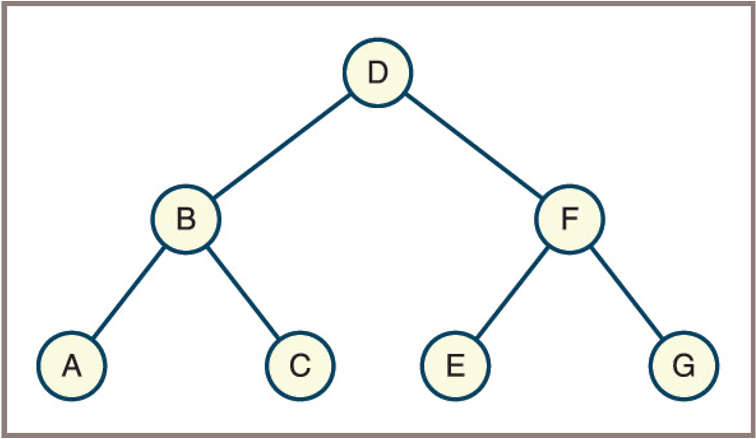
  • A binary representation of a sorted collection that contains the letters A through G (Also called Binary Search Tree - BST)

The Shape of Binary Trees

  • Trees as data structures come in various shapes and sizes
    • Some are vine-like and some are bushy
  • The shape of a binary tree can be described by specifying the relationship between its height and the number of nodes it contains
    • A binary tree can be vine-like with N nodes and a height of N − 1
    • A full binary tree contains the full complement of nodes at each level

The Shape of Binary Trees

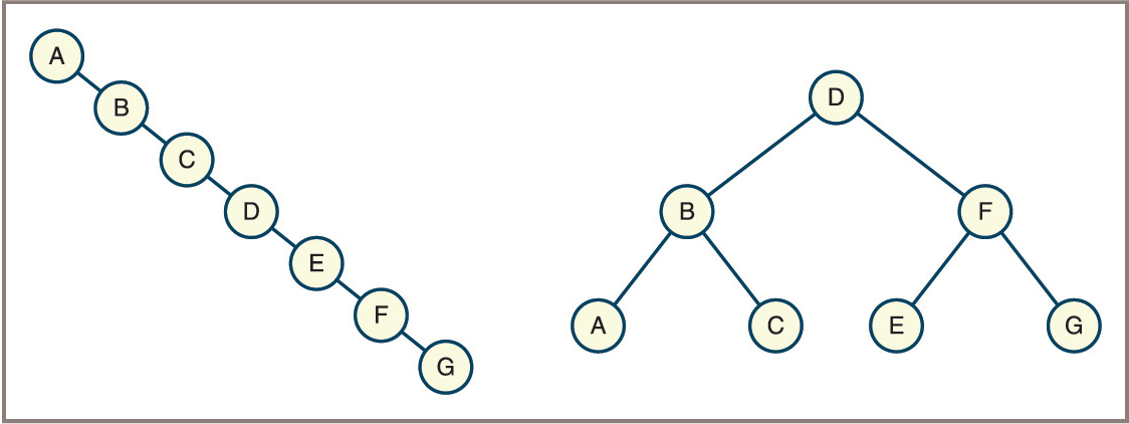
  • A vine-like tree is a binary tree where each node has at most one child, resulting in a structure similar to a linked list (maximum height, minimum bushiness).
  • A bushy tree is a binary tree where nodes have two children as often as possible, resulting in a more balanced and compact structure (minimum height, maximum bushiness).

The Shape of Binary Trees

  • The Relationship Between the Height and the Number of Nodes in Full Binary Tree
Height (h) Minimum Nodes Maximum Nodes (Full Binary Tree)
0 1 1
1 2 3
2 3 7
3 4 15
h h + 1 2^(h+1) - 1
  • In a full binary tree of height h, the maximum number of nodes is 2^(h+1) - 1.
  • The minimum number of nodes in a binary tree of height h is h + 1 (vine-like tree).

The Shape of Binary Trees

  • Not all bushy trees are full binary trees
    • However, a perfectly balanced binary tree, is bushy enough to support worst-case logarithmic access to leaf nodes
  • A complete binary tree, in which any nodes on the last level are filled in from left to right, is, like a full binary tree
    • A special case of a perfectly balanced binary tree

The Shape of Binary Trees

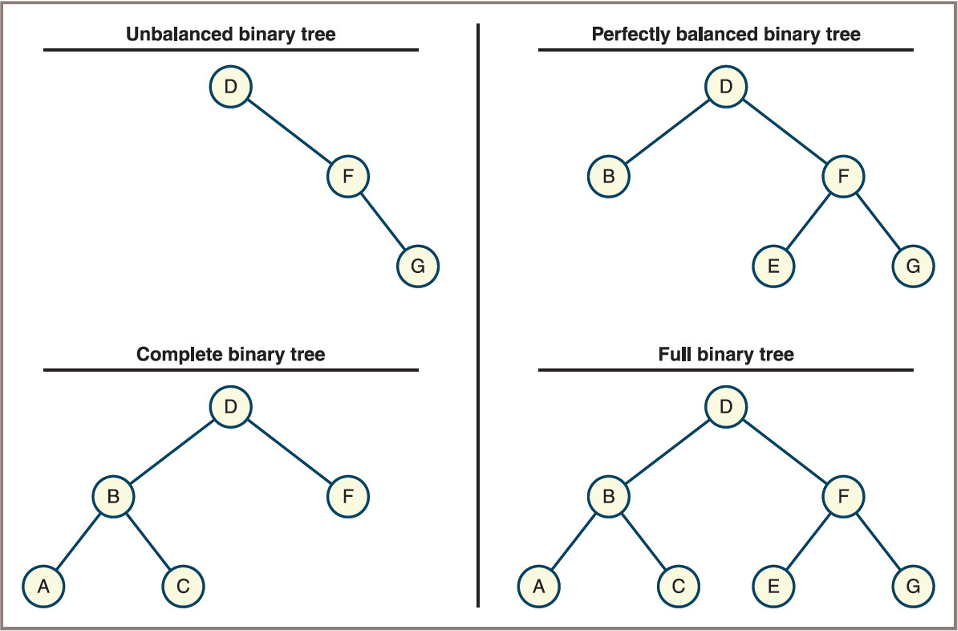
  • Four types of shapes of binary trees

Binary Tree Traversals

  • Four standard types of traversals for binary trees:
    • Preorder
    • Inorder
    • Postorder
    • Level order
  • Each type follows a particular path and direction as it visits the nodes in the tree

Binary Tree: Preorder Traversals

  • Preorder traversal visits nodes in the following order:

    1. Visit the root node.
    2. Traverse the left subtree in preorder.
    3. Traverse the right subtree in preorder.

  • Pseudocode:

    Preorder(node):
    if node is not null:
        visit(node)
        Preorder(node.left)
        Preorder(node.right)

Binary Tree: Preorder Traversals

  • Example:
    For the tree below, the preorder traversal order is: D, B, A, C, F, E, G

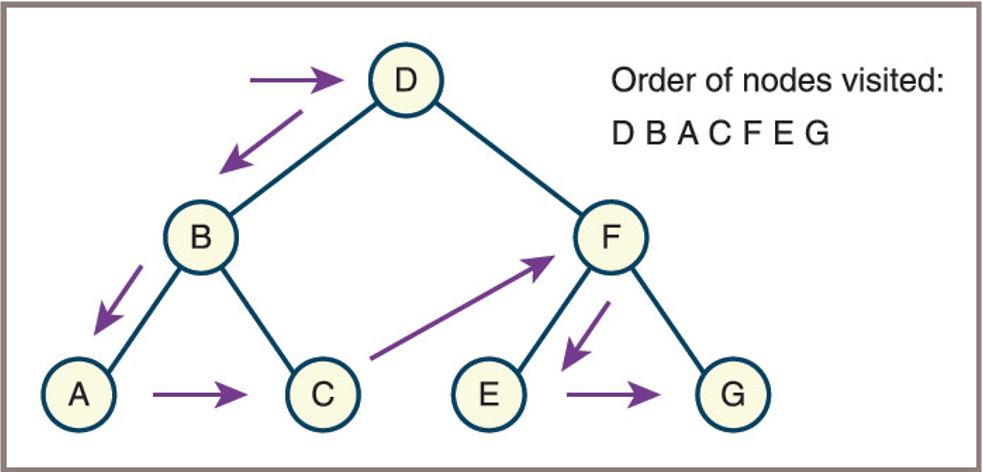
Binary Tree: Inorder Traversals

  • Inorder traversal visits nodes in the following order:
    1. Traverse the left subtree in inorder.
    2. Visit the root node.
    3. Traverse the right subtree in inorder.
  • Pseudocode:
Inorder(node):
    if node is not null:
        Inorder(node.left)
        visit(node)
        Inorder(node.right)

Binary Tree: Inorder Traversals

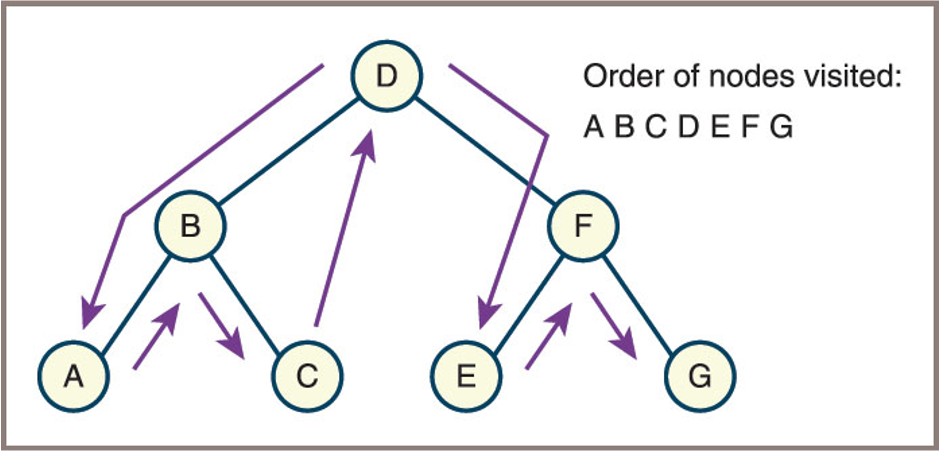
  • Example:
    For the tree below, the inorder traversal order is: A, B, C, D, E, F, G

Binary Tree: Postorder Traversals

  • Postorder traversal visits nodes in the following order:
    1. Traverse the left subtree in postorder.
    2. Traverse the right subtree in postorder.
    3. Visit the root node.
  • Pseudocode:
Postorder(node):
    if node is not null:
        Postorder(node.left)
        Postorder(node.right)
        visit(node)

Binary Tree: Postorder Traversals

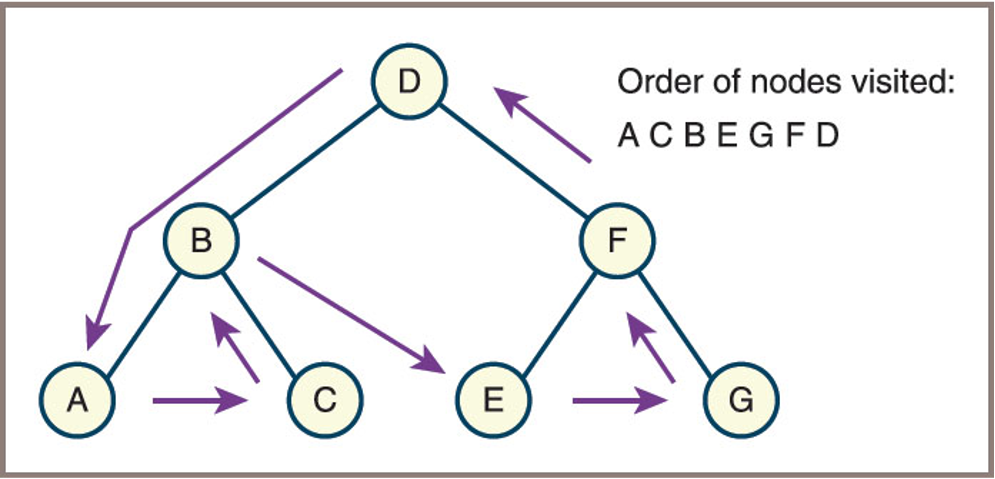
  • Example:
    For the tree below, the postorder traversal order is: A, C, B, E, G, F, D

Binary Tree: Level Order Traversals

  • Level order traversal visits nodes level by level from top to bottom and left to right within each level.

  • This traversal uses a queue data structure.

  • Pseudocode:

LevelOrder(root):
    if root is not null:
        for each level from 0 to height of tree:
            visit all nodes at that level from left to right

Binary Tree: Level Order Traversals

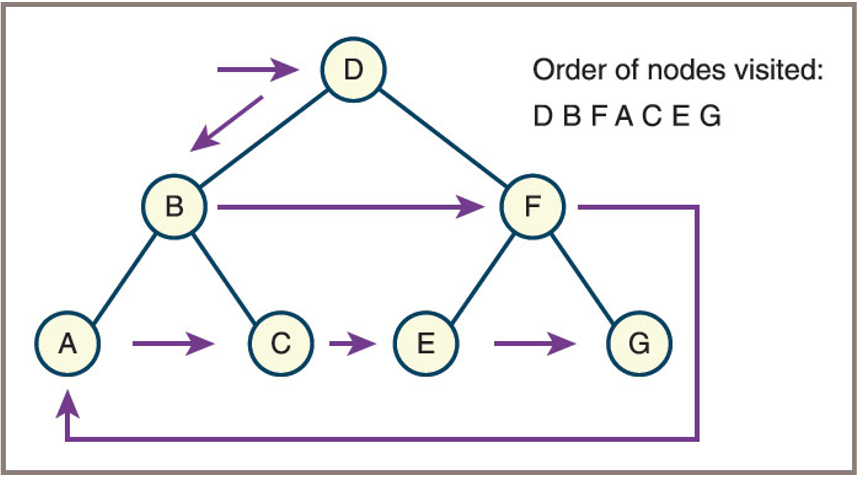
  • Example:
    For the tree below, the level order traversal order is: D, B, F, A, C, E, G

Read up: Common Applications of Binary Trees