Stacks Application

Fred Agbo

2025-10-13

Announcements

  • Welcome to week 8!
  • Midterm exam is this week Wednesday during class hours (1:10 - 20:40 pm)
    • Those with AES accommondation:
      • Contact the testing center ASAP to book a spot for the test.
      • Copy me in the email to the Testing Center
      • No correspondence from Testing Center means you’re taking the exam in class
    • Solution to practice questions are posted on Canvas

Application of Stack: Backtracking!

What is a Backtracking Algorithm?

  • A backtracking algorithm is a general algorithmic technique that considers searching every possible combination in order to solve a computational problem.
  • It incrementally builds candidates to the solutions and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly lead to a valid solution.
  • Commonly used for problems like puzzles, pathfinding, and combinatorial optimization (e.g., Sudoku, N-Queens, Maze solving).

What is a Backtracking Algorithm?

  • Begins in a predefined starting state and moves from state to state in search of a desired ending state
  • If the algorithm reaches a state that represents an undesirable outcome, it backs up to the last point at which there was an unexplored alternative and tries it
  • Two principal techniques for implementing backtracking algorithms
    • One uses stacks
    • The other uses recursion

Backtracking Algorithm

  • The role of a stack in the process is to remember the alternative states that occur at each juncture:
    • Consider the problem of finding a path out of a maze

Sample backtracking algorithm:

Create a new stack
Locate the character 'P' in the grid
Push its location onto the stack
While the stack is not empty
    Pop a location, (row, column), off the stack
    If the grid contains 'T' at this location, then
        A path has been found
        Return True
    Else if this location does not contain a dot
        Place a dot in the grid at this location
        Examine the adjacent cells to this one and
        for each one that contains a space,
            push its location onto the stack
Return False

Memory Management (1/7)

  • During a program’s execution, both its code and its data occupy computer memory
  • The computer’s run-time system must keep track of various details that are invisible to the program’s author, which include the following:
    • Associating variables with data objects stored in memory so they can be located when these variables are referenced
    • Remembering the address of the instruction in which a method or function is called, so control can return to the next instruction when that function or method finishes execution
    • Allocating memory for a function’s or a method’s arguments and temporary variables, which exist only during the execution of that function or method

Memory Management (2/7)

  • A Python compiler translates a Python program into bytecodes:
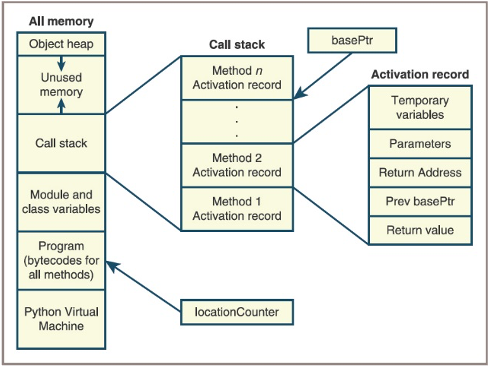
  • A complex program called the Python Virtual Machine (PVM) then executes these
  • The memory, or run-time environment, controlled by the PVM is divided into six regions:
    • Object heap
    • Unused memory
    • Call stack
    • Module and class variables
    • Program bytecode for all methods
    • Python Virtual Machine

Memory Management (3/7)

  • Architecture of a run-time environment

Memory Management (4/7)

  • The activation records shown in the figure contain two types of information:
    • The regions labeled Temporary Variables and Parameters hold data needed by the executing subroutine
    • The remaining regions hold data that allow the PVM to pass control backward from the currently executing subroutine to the subroutine that called it

Memory Management (5/7)

  • When a subroutine is called, the PVM performs the following steps:
    • Creates the subroutine’s activation record and pushes it onto the call stack
    • Saves the basePtr’s current value in the region labeled Prev basePtr and sets the basePtr to the new activation record’s base
    • Saves the locationCounter’s current value in the region labeled Return Address and sets the locationCounter to the first instruction of the called subroutine
    • Copies the calling parameters into the region labeled Parameters
    • Starts executing the called subroutine at the location indicated by the locationCounter

Memory Management (6/7)

  • When a subroutine has finished executing, the PVM performs the following steps:
    • Reestablishes the settings needed by the calling subroutine by restoring the values of the locationCounter and the basePtr from values stored in the activation record
    • Pops the activation record from the call stack
    • Resumes execution of the calling subroutine at the location indicated by the locationCounter

Memory Management (7/7)

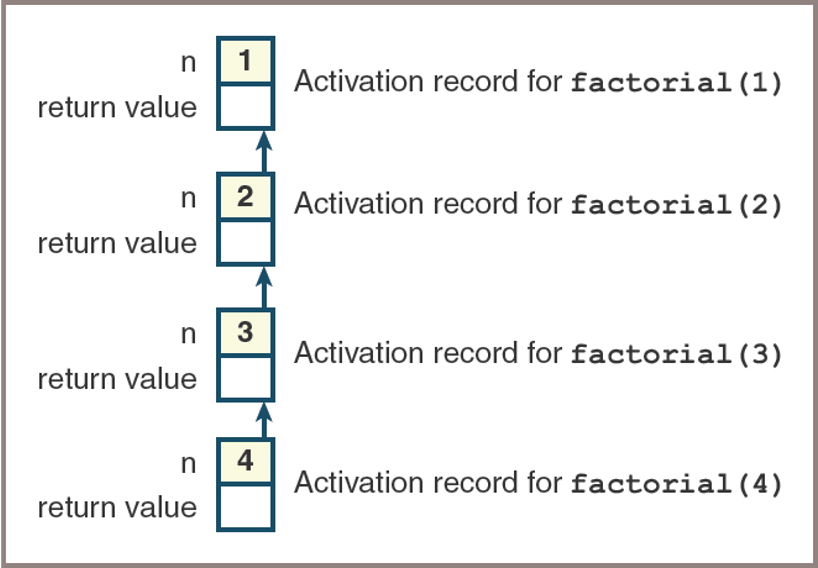
  • Example of recursive Factorial:
def factorial(n):
    if n == 1:
    return 1
    else:
    return n * factorial(n – 1)

Stacks Implementations

  • Stacks are implemented easily using arrays or linked structures
  • The following sections show that there are trade-offs involved in using these two recurring approaches
    • Two stack implementations are the classes ArrayStack and LinkedStack
    • Before we develop these, you are provided with a short tester program that shows how you can test them immediately
      • The code, provided in a couple of slides from here, exercises all the methods in any stack implementation and gives you an initial sense that they are working as expected:

Stacks Implementations

  • Implementation of stacks uses inheritance concepts:
    • A base class defines common stack behaviors and properties.
    • Subclasses (ArrayStack, LinkedStack) inherit from the base class and provide specific implementations.
    • This promotes code reuse and enforces a consistent interface for different stack types.
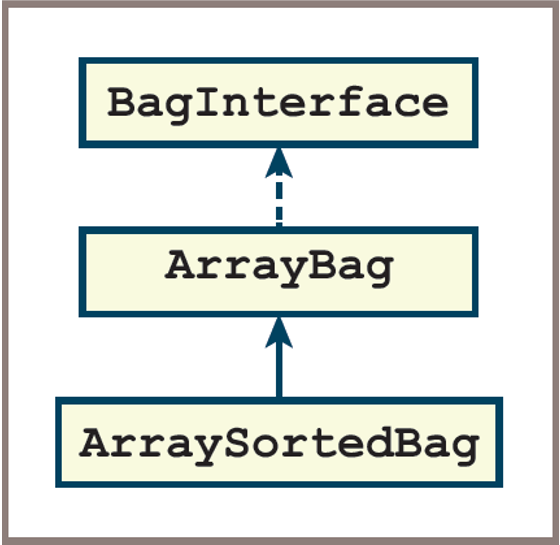
  • Consider we want to make ArraySortedBag class, a subclass of the ArrayBag class:
    • ArrayBag is called the parent or superclass of ArraySortedBag
    • Because the ArrayBag class implements BagInterface, the ArraySortedBag class also implements this interface via inheritance

Inheritance: Subclassing an Existing Class

  • This diagram depicts a subclass and inheritance in a class diagram

    • Class diagram showing inheritance in object-oriented programming. The diagram displays a parent class labeled ArrayBag with an arrow pointing to a subclass labeled ArraySortedBag, indicating that ArraySortedBag inherits from ArrayBag. The environment is a simple diagram with labeled boxes and connecting arrows, focusing on the relationship between the two classes. No emotional tone is present.

Inheritance: Subclassing an Existing Class

  • To create a subclass of an existing class consists the following steps:
    • Make a copy of the parent’s class file
    • Begin by deleting all the methods that do not have to change:
    • You still need the _init_ method in the new class
    • To guarantee that the inheritance happens, you must place the name of the parent class within the parentheses of the class header
    • Modify the code for the methods that must change
    • Add any new methods

Inheritance: Subclassing an Existing Class

  • There is one case where inheritance is not automatic
    • From the figure above, the _init_ method in ArraySortedBag must call the _init_ method in the parent class ArrayBag
      • So that it can initialize the data contained there
    • The syntax to call this method in the parent class is ArrayBag._init_(self, sourceCollection)
  • The parent class name enables Python to select which version of the _init_ method to run
  • Note the additional argument, self, at the beginning of the argument list
  • The optional source collection is also passed as an argument to the parent class’s _init_ method

ArrayBag and ArraySortedBag Example

  • Code for the changes to ArraySortedBag so far:
from arraybag import ArrayBag
 
class ArraySortedBag(ArrayBag):
    """An array-based sorted bag implementation."""
 
    # Constructor
    def __init__(self, sourceCollection = None):
        """Sets the initial state of self, which includes the
        contents of sourceCollection, if it’s present."""
        ArrayBag.__init__(self, sourceCollection)

Using Inheritance to implement Stacks

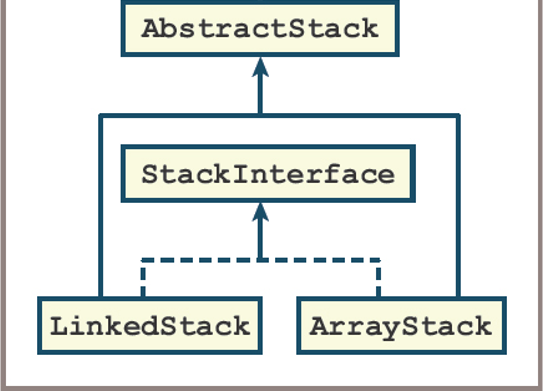
  • ArrayStack and LinkedStack
    • Implement the same interface, called StackInterface
    • Are subclasses of the AbstractStack class, which in turn is a subclass of AbstractCollection
    • Inherit the add method from the AbstractStack class, the size variable, and the methods isEmpty, __len__, __str__, __add__, and __eq__ from AbstractCollection
    • The only methods that need to be implemented in ArrayStack and LinkedStack are _init_, peek, push, pop, clear, and _iter_

Stacks Collections Hierarchy

  • The stack resources in the collection hierarchy

Implementing AbtractStack

class AbstractStack(object):
    """Abstract class that implements the common 
    methods for stack collections"""
    
    # Constructor
    def __init__(self, sourceCollection=None):
        self.size = 0
        if sourceCollection:
            for i in sourceCollection:
                self.push(i)
                
    def isEmpty(self):
        """Returns True if stack is empty. Otherwise, returns False 
        """
        return len(self) == 0
    
    def __len__(self):
        """Returns the number of items in stack
        """
        return self.size
    
    def __str__(self):
        """Returns the string repsentative of S
        """
        return "{" + ", ".join(map(str,self)) +"}"

Implementing ArrayStacks

from arrays import Array
from abstractstack import AbstractStack

class ArrayStack(AbstractStack):
    "Array-based stack collections"
    
    # Array inital capacity
    DEFAULT_CAPACITY = 10
    
    #Constructor
    """Initializes the state of self which include any items from sourcecollector"""
    def __init__(self, sourceCollection = None):
        self.items = Array(ArrayStack.DEFAULT_CAPACITY)
        AbstractStack.__init__(self, sourceCollection)
    
    # Accessors 
    def __iter__(self):
        """Supports iteration over self. Visits items bottom to top of stack"""
        cursor =0
        while cursor < len(self):
            yield self.items[cursor]
            cursor +=1
    
    def peek(self):
        if self.isEmpty():
            raise KeyError("The stack is empty") 
        return self.items[len(self)-1]
    
    # Mutator functions
    def push(self, item):
        #resize the array here if neccesary
        self.items[len(self)] = item
        self.size +=1
        
    def clear(self):
        self.size =0
        self.items = Array(ArrayStack.DEFAULT_CAPACITY)
        
    def pop(self):
        #Check the precondition that the stack is not empty
        if self.isEmpty():
            raise KeyError("The stack is empty") 
        oldItem = self.items[len(self)-1]
        self.size -=1
        # resize the Array here if necessary
        return oldItem

Testing ArrayStacks

"""
A tester program for stack implementations.
"""
from arraystack import ArrayStack
#from linkedstack import LinkedStack

def test(stackType):
    # Test any implementation with the same code
    s = stackType()
    print("Length:", len(s))
    print("Empty:", s.isEmpty())
    print("Push 1-12")
    for i in range(12):
        s.push(i + 1)
    print("Peeking:", s.peek())
    print("Items (bottom to top):", s)
    print("Length:", len(s))
    print("Empty:", s.isEmpty())
    theClone = stackType(s)
    print("Items in clone (bottom to top):", theClone)
    theClone.clear()
    print("Length of clone after clear:", len(theClone))
    print("Push 11")
    s.push(11)
    print("Popping items (top to bottom):", end = " ")
    while not s.isEmpty(): print(s.pop(), end = " ")
    print("\nLength:", len(s))
    print("Empty:", s.isEmpty())
test(ArrayStack)
#test(LinkedStack)

Array Stacks Implementations

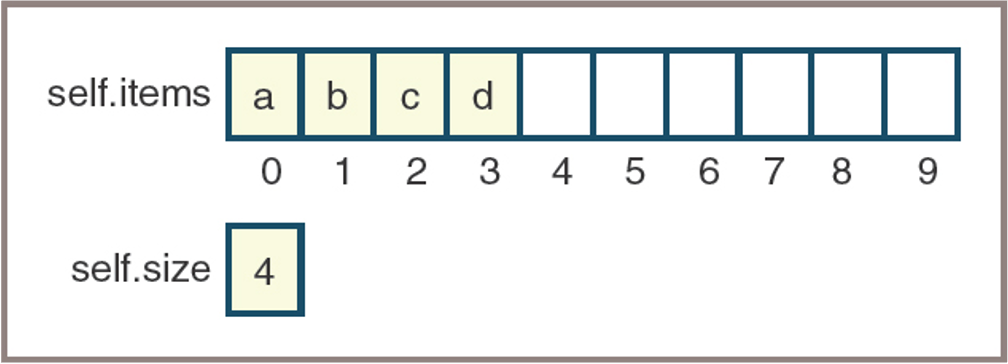
  • The first implementation is built around an array called self.items and an integer called self.size
  • shows how self.items and self.size appear when four items are on the stacks

Linked Stacks Implementations

  • The linked implementation requires two classes:
    • LinkedStack and Node
  • The Node class contains two fields:
    • data — An item on the stack
    • next — A pointer to the next node
  • Because new items are added to and removed from just one end of the linked structure, the methods pop and push are easy to implement, as shown in Figures on the next slides.

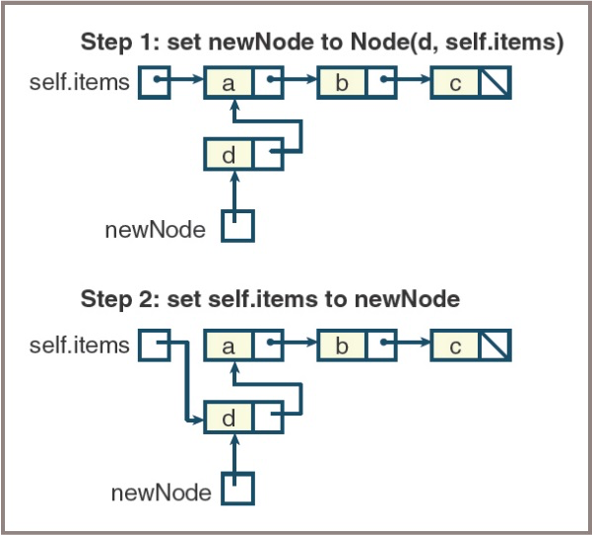
Linked Stacks Implementations

  • Pushing an item onto a linked stack

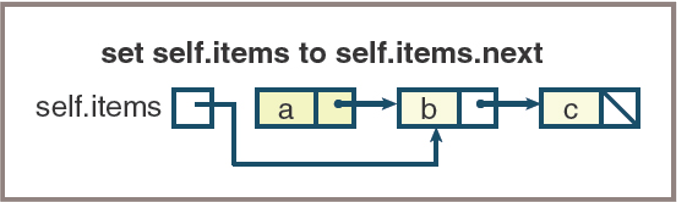
Linked Stacks Implementations

  • Popping an item from a linked stack