STACKS

Fred Agbo

2025-10-06

Announcements

Welcome to week 7!
Week 5-7 assignment (Problem set 3) is posted and due on Wednesday 8
Midterm exam is next week Wednesday during class hours
- Those with AES accommondation should contact the testing center ASAP to book a spot for the test.
- Copy me in the email to the Testing Center
- Generally, I’ll prefer the booking at Testing Center to be same day of the exam or within the week (Thu or Fri)

Learning Objectives

Describe the features and behavior of a stack
Choose a stack implementation based on its performance characteristics
Recognize applications where it is appropriate to use a stack
Explain how the system call stack provides run-time support for recursive subroutines
Design and implement a backtracking algorithm that uses a stack

Overview of Stacks

Stacks - Linear Collection
- A stack is a linear data structure that follows the Last-In, First-Out (LIFO) principle.
  - This means that the last element added to the stack will be the first one to be removed.
Analogy
- Stack of clean trays in a cafeteria
  - New tray is removed from top of the stack, when needed

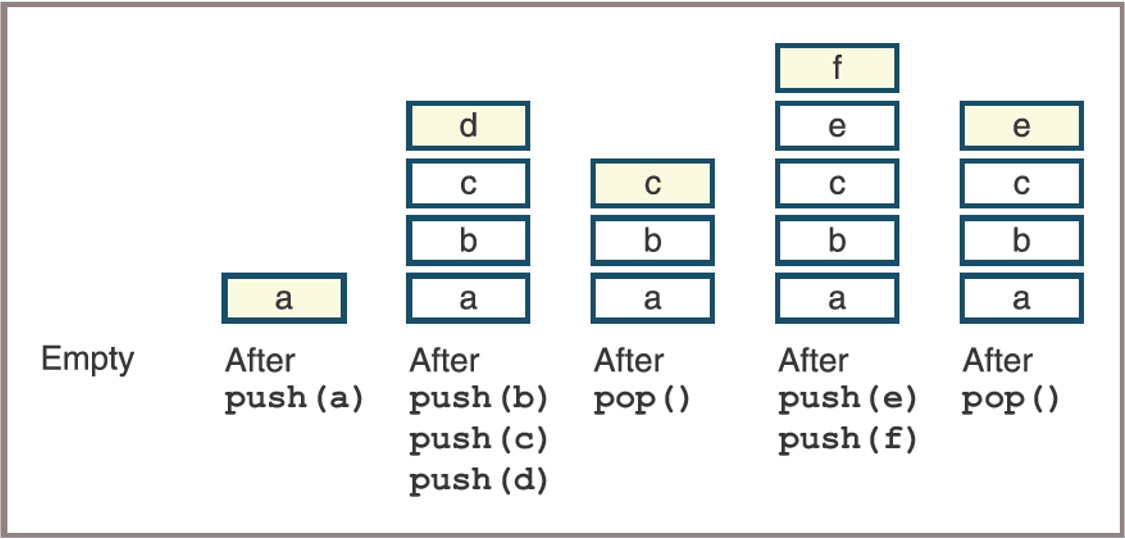
Overview of Stacks

Some states in the lifetime of a stack

Overview of Stacks

Operations
- Push: Add an item to the top of the stack.
- Pop: Remove the item from the top of the stack.
- Peek/Top: View the item at the top without removing it.

Common Application of `Stacks` in CS

Function call management (call stack): managing computer memory in support of function and method calls
Undo mechanisms in editors: word processors, spreadsheet programs, etc
Syntax parsing (e.g., matching parentheses)
Translating infix expressions to postfix form and evaluating postfix expressions
Backtracking algorithms
Maintaining a history of the links visited by a web browser

Using a Stack

A stack type is not built into Python
Programmers can use a Python list to emulate an array-based stack:
- The list method append pushes an element onto this stack
- The list method pop removes and returns the element at its top
The main drawback of this option is as follows:
- All other list operations can manipulate the stack as well

Using a Stack

To use a stack, you typically need to:
1. Create an empty stack.
2. Push items onto the stack as needed.
3. Pop items off the stack when you need to process or remove them.
4. Peek at the top item to see what is next to be processed (optional).
5. Check if the stack is empty before popping or peeking.

The Stack Interface

A stack typically provides the following interface:
- An operation named peek for examining the element at the top of a stack
- The stack type can also include operations such as
  - clear
  - isEmpty
  - len
  - str
  - in
  - +
These operations are listed as Python methods in next slide

The Stack Interface

Stack Method	What It Does
`s.isEmpty()`	Returns True if `s` is empty or False otherwise.
`s.__len__()`	Same as `len(s)`. Returns the number of items in `s`.
`s.__str__()`	Same as `str(s)`. Returns the string representation of `s`.
`s.__iter__()`	Same as `iter(s)`, or `for item in s:`. Visits each item in `s`, from bottom to top.
`s.__contains__(item)`	Same as `item in s`. Returns True if `item` is in `s` or False otherwise.
`s1.__add__(s2)`	Same as `s1 + s2`. Returns a new stack containing the items in `s1` and `s2`.
`s.__eq__(anyObject)`	Same as `s == anyObject`. Returns True if `s` and `anyObject` are equal.
`s.clear()`	Makes `s` become empty.
`s.peek()`	Returns the item at the top of `s`. Precondition: `s` must not be empty; raises a KeyError if the stack is empty.
`s.push(item)`	Adds `item` to the top of `s`.
`s.pop()`	Removes and returns the item at the top of `s`. Precondition: `s` must not be empty; raises a KeyError if the stack is empty.

"""
File: baginterface.py
Author: Ken Lambert
"""
 
class BagInterface(object):
    """Interface for all bag types."""
 
    # Constructor
    def __init__(self, sourceCollection = None):
        """Sets the initial state of self, which includes the
        contents of sourceCollection, if it’s present."""
        pass
 
    # Accessor methods
    def isEmpty(self):
        """Returns True if len(self) == 0,
        or False otherwise."""
        return True
 
    def __len__(self):
        """Returns the number of items in self."""
        return 0
 
    def __str__(self):
        """Returns the string representation of self."""
        return ""
 
    def __iter__(self):
        """Supports iteration over a view of self."""
        return None
    def __add__(self, other):
        """Returns a new bag containing the contents
        of self and other."""
        return None
 
    def __eq__(self, other):
        """Returns True if self equals other,
        or False otherwise."""
        return False
     
    def count(self, item):
        """Returns the number of instances of item in self."""
        return 0
 
    # Mutator methods
    def clear(self):
        """Makes self become empty."""
        pass
 
    def add(self, item):
        """Adds item to self."""
        pass
 
    def remove(self, item):
        """Precondition: item is in self.
        Raises: KeyError if item in not in self.
        Postcondition: item is removed from self."""
        pass

## Another Python Stack Interface Example

from abc import ABC, abstractmethod

class Stack(ABC):
        @abstractmethod
        def isEmpty(self):
                pass

        @abstractmethod
        def __len__(self):
                pass

        @abstractmethod
        def __str__(self):
                pass

        @abstractmethod
        def __iter__(self):
                pass

        @abstractmethod
        def __contains__(self, item):
                pass

        @abstractmethod
        def __add__(self, other):
                pass

        @abstractmethod
        def __eq__(self, other):
                pass

        @abstractmethod
        def clear(self):
                pass

        @abstractmethod
        def peek(self):
                pass

        @abstractmethod
        def push(self, item):
                pass

        @abstractmethod
        def pop(self):
                pass

Stack Operations: A walk-through

Operation	State of Stack after the Operation	Value Returned	Comment
`s = <Stack Type>()`			Initially, stack is empty.
`s.push('a')`	a		The stack contains the single item.
`s.push('b')`	ab		b is the top item.
`s.push('c')`	abc		c is the top item.
`s.isEmpty()`	abc	False	The stack is not empty.
`len(s)`	abc	3	The stack contains three items.
`s.peek()`	abc	c	Return the top item without removing it.

Stack Operations: A walk-through

Operation	State of Stack after the Operation	Value Returned	Comment
`s.pop()`	ab	c	Remove and return the top item. b is now the top item.
`s.pop()`	a	b	Remove and return the top item. a is now the top item.
`s.pop()`		a	Remove and return the top item.
`s.isEmpty()`		True	The stack is empty.
`s.peek()`		KeyError	Peeking at an empty stack raises an exception.
`s.pop()`		KeyError	Popping an empty stack raises an exception.
`s.push('d')`	d		d is the top item.

Instantiating a Stack

Later in this chapter, two different implementations are considered:
- ArrayStack
- LinkedStack
For now, let us assume they are existing
- This code segment shows how you might instantiate them:
  - s1=ArrayStack ()
  - s2=LinkedStack ([20, 40, 60])

Stack Application: Matching Parentheses

One classic application of stacks is checking for balanced parentheses (and other brackets) in expressions.
- Compilers need to determine if the bracketing symbols in expressions are balanced correctly
The algorithm uses a stack to keep track of opening brackets as they appear.
When a closing bracket is encountered, the stack is checked to ensure it matches the most recent opening bracket.
The Table in the next slide provides some examples:

Matching Parentheses

Balanced and Unbalanced Brackets in Expressions

Example Expression	Status	Reason
`(…)….(…)`	Balanced
`(…)….(…`	Unbalanced	Missing a closing `)` at the end
`)…(...(…)`	Unbalanced	The closing `)` at the beginning has no matching opening `(` and one opening has no closing
`[…(…)…]`	Balanced
`[…(…]…)`	Unbalanced	The bracketed sections are not nested properly

Matching Parentheses

To check an expression, take the following steps:
- Scan across the expression, pushing opening brackets onto a stack
- On encountering a closing bracket, if the stack is empty or if the item on the top of the stack is not an opening bracket of the same type, you know the brackets do not balance; therefore, you can quit the process and signal that the expression is improperly formed
- Otherwise, pop the item off the top of the stack and continue scanning the expression
- When you reach the end of the expression, the stack should be empty, and if it is not, you know the brackets do not balance

Stack Application:

Three Areas:
- First, you’ll see algorithms for evaluating arithmetic expressions:
- These algorithms apply to problems in compiler design, and you will use them in the chapter’s case study
- Second, you’ll learn a general technique for using stacks to solve backtracking problems:
  - The programming projects explore applications of the technique
- Third, you’ll witness the role of stacks in computer memory management

Evaluating Arithmetic Expressions (1/3)

An indirect approach to evaluating arithmetic expressions works best:
- Transform an expression from its familiar infix form to a postfix form
- Evaluate the postfix form
- In the infix form, each operator is located between its operands In the postfix form, an operator immediately follows its operands

Evaluating Arithmetic Expressions (2/3)

Some Infix and Postfix Expressions

Infix Form	Postfix Form	Value
34	34	34
34 + 22	34 22 +	56
34 + 22 * 2	34 22 2 * +	78
34 * 22 + 2	34 22 * 2 +	750
(34 + 22) * 2	34 22 + 2 *	112

Evaluating Arithmetic Expressions (3/3)

Consider the steps in evaluating the following:
- Infix evaluation: 34 + 22 * 2 → 34 + 44 → 78
- Postfix evaluation: 34 22 2 * + → 34 44 + → 78
The use of parentheses and operator precedence in infix expressions is for the convenience of the human beings who read them and write them
By eliminating these parentheses, The equivalent postfix expressions present a computer with a format that is much easier and more efficient for it to evaluate

Evaluating Postfix Expressions (1/2)

Evaluating a postfix expression involves three steps:
- Scan across the expression from left to right
- On encountering an operator, apply it to the two preceding operands and replace all three by the result
- Continue scanning until you reach the expression’s end, at which point only the expression’s value remains

Evaluating Postfix Expressions (2/2)

Tracing the Evaluation of a Postfix Expression : 4 5 6 * +3 −

Portion of Postfix Expression Scanned So Far	Operand Stack	Comment
		No tokens have been scanned yet, so the stack is empty
4	4	Push the operand 4
4 5	4 5	Push the operand 5
4 5 6	4 5 6	Push the operand 6
4 5 6 *	4 30	Replace the top two operands by their product
4 5 6 * +	34	Replace the top two operands by their sum
4 5 6 * + 3	34 3	Push the operand 3
4 5 6 * + 3 -	31	Replace the top two operands by their difference and pop the final value

Converting Infix to Postfix (1/2)

Detailed steps
- Start with an empty postfix expression and an empty stack, which will hold operators and left parentheses
- Scan across the infix expression from left to right
- On encountering an operand, append it to the postfix expression
- On encountering a left parenthesis, push it onto the stack
- On encountering an operator, pop off the stack all operators that have equal or higher precedence, append them to the postfix expression, and then push the scanned operator onto the stack
- On encountering a right parenthesis, shift operators from the stack to the postfix expression until meeting the matching left parenthesis, which is discarded
- On encountering the end of the infix expression, transfer the remaining operators from the stack to the postfix expression

Converting Infix to Postfix (2/2)

Tracing the Conversion of an Infix Expression 4 + 5 * 6 − 3 to a Postfix Expression

Portion of Infix Expression Scanned So Far	Operator Stack	Postfix Expression	Comment
			No tokens have been scanned yet, so the stack and PE are empty
4		4	Append 4 to the PE
4 +	+	4	Push + onto the stack
4 + 5	+	4 5	Append 5 to the PE
4 + 5 *	+ *	4 5	Push * onto the stack
4 + 5 * 6	+ *	4 5 6	Append 6 to the PE
4 + 5 * 6 −	−	4 5 6 * +	Pop * and +, append them to the PE, and push – onto the stack
4 + 5 * 6 − 3	−	4 5 6 * + 3	Append 3 to the PE
4 + 5 * 6 − 3 (end)		4 5 6 * + 3 −	Pop the remaining operators off the stack and append them to the PE

STACKS

Announcements

Learning Objectives

Overview of Stacks

Overview of Stacks

Overview of Stacks

Common Application of Stacks in CS

Using a Stack

Using a Stack

The Stack Interface

The Stack Interface

Stack Operations: A walk-through

Stack Operations: A walk-through

Instantiating a Stack

Stack Application: Matching Parentheses

Matching Parentheses

Matching Parentheses

Stack Application:

Evaluating Arithmetic Expressions (1/3)

Evaluating Arithmetic Expressions (2/3)

Evaluating Arithmetic Expressions (3/3)

Evaluating Postfix Expressions (1/2)

Evaluating Postfix Expressions (2/2)

Converting Infix to Postfix (1/2)

Converting Infix to Postfix (2/2)

Backtracking!

Common Application of `Stacks` in CS