ARRAYS

Fred Agbo

2025-09-15

Announcements

• Welcome back!
• First Mini-project (MP1) is due on Wednesday at 10pm
• Reading for this week is due on Wednesday

Arrays

Learning Objectives

• Create arrays
• Perform various operations on arrays
• Determine the running times and memory usage of array operations
• Describe how costs and benefits of array operations depend on how arrays are represented in computer memory

Array Data Structure

• Array – represents a sequence of items that can be accessed or replaced at given index positions:
  • Data structure underlying a Python list is an array
  • It is the primary implementing structure in the collections of Python
  • In Python we call them lists
  • In other languages, all values in an array must have the same type (e.g., integers, strings), which are more memory-efficient and faster for numeric operations.

Array Data Structure

• A programmer can:
  • Access and replace an array’s items at given positions
  • Examine an array’s length
  • Obtain its string representation
• A programmer cannot
  • Add or remove positions
  • Make the length of the array larger or smaller (length of an array is fixed when created)

Array review

• The values are accessed by a numerical index between 0 and array size minus 1
• To reference a single array/list element, use arrayName[index]
• The array index is sometimes called a subscript.

Python Arrays: List[]

• In Python, the term “array” usually refers to either a list or the array module’s array type. Here are the main characteristics:
  • Python lists are dynamic arrays: they can store elements of different types, grow or shrink in size, and support indexing, slicing, and iteration.
  • Lists are not memory-efficient for large numeric data; for that, use the array module or NumPy arrays.
• The array module provides arrays that store elements of a single type (e.g., all integers or all floats)

Python Arrays vs Traditional Arrays

• Both types support random access (O(1) time for getting/setting elements by index).

• Lists and arrays are mutable: you can change, add, or remove elements.

• Type Consistency:

  • Traditional arrays (e.g., in C, Java) store elements of a single, fixed type.
  • Python lists (often called “arrays”) can store elements of different types in the same list.

Python Arrays vs Traditional Arrays

• Memory Layout:
  • Traditional arrays use contiguous memory, making them efficient for random access and low-level operations.
  • Python lists are dynamic and store references to objects, not the objects themselves, so memory is less compact.
• Size:
  • Traditional arrays have a fixed size; you cannot change their length after creation.
  • Python lists are dynamic; you can add or remove elements at any time.

Python Arrays vs Traditional Arrays

• Performance:
  • Traditional arrays are faster for numeric operations and use less memory.
  • Python lists are flexible but slower and less memory-efficient for large numeric data.
• Built-in Support:
  • Python has a built-in list type (dynamic array) and an array module for fixed-type arrays.
  • For scientific computing, NumPy arrays provide efficient, fixed-type arrays similar to traditional arrays.

Python Array Class

• Python’s array model includes an array class:
• You will define a new class named Array that adheres to the restrictions mentioned earlier but can hold items of any type
• This Array class uses a Python list to hold its items
• The class defines methods that allow clients to use
  • The subscript operator []
  • The len function
  • The str function
  • The for loop with array objects

Operations and methods of Python Array Class

User’s Array Operation	Method in the Array Class
a = Array(10)	init(capacity, fillValue=None)
len(a)	len()
str(a)	str()
for item in a:	iter()
a[index]	getitem(index)
a[index] = newitem	setitem(index, newItem)

Python Array Class Implementation

"""
File: arrays.py
An Array is like a list, but the client can use
only [], len, iter, and str.
 
To instantiate, use
<variable> = Array(<capacity>, <optional fill value>)
 
The fill value is None by default.
"""

class Array(object):
    """Represents an array."""
 
    def __init__(self, capacity, fillValue = None):
        """Capacity is the static size of the array.
        fillValue is placed at each position."""
        self.items = list()
        for count in range(capacity):
            self.items.append(fillValue)

    def __len__(self):
        """-> The capacity of the array."""
        return len(self.items)
     
    def __str__(self):
        """-> The string representation of the array."""
        return str(self.items)
     
    def __iter__(self):
        """Supports traversal with a for loop."""
        return iter(self.items)
     
    def __getitem__(self, index):
        """Subscript operator for access at index."""
        return self.items[index]
     
    def __setitem__(self, index, newItem):
        """Subscript operator for replacement at index."""
        self.items[index] = newItem

Sample use of Array class

from arrays import Array

a = Array(5)    # Create an array with 5 positions
len(a)  # Show the number of positions
5
print(a)    # Show the contents
[None, None, None, None, None]
for i in range(len(a)): # Replace contents with 1..5
    a[i] = i + 1
a[0]    # Access the first item
1
for item in a:  # Traverse the array to print all
print(item)
1
2
3
4
5

Developing a class called Array

Why is this needed?

• Can’t we use Python’s list type instead?
  • We want to study the performance and behavior of fundamental (traditional) data structures
  • The built-in list type is a class that contains too much complexity and hides what is really happening
• We will create a simple class that models the behavior of a simple array, and that suppresses (hides) the features of Python’s list

Fundamental Array class design

• Attributes (see in the next slides):
  • A list __a to store the elements of the array
  • A number __nItems to keep track of how many elements of a have been used so far.
• Some of the methods:
  • __init__ - constructor
  • insert – insert an item at end of the Array
  • get – retrieves the i’th element of the Array
  • find – find an item in the Array
  • delete – removes an item from the Array
  • __str__ – return a string representation of the Array

Unordered array class

• Implementation

• Client uses the class to create a new array:

# Create an Array with room for 100 elements
x = Array(100)

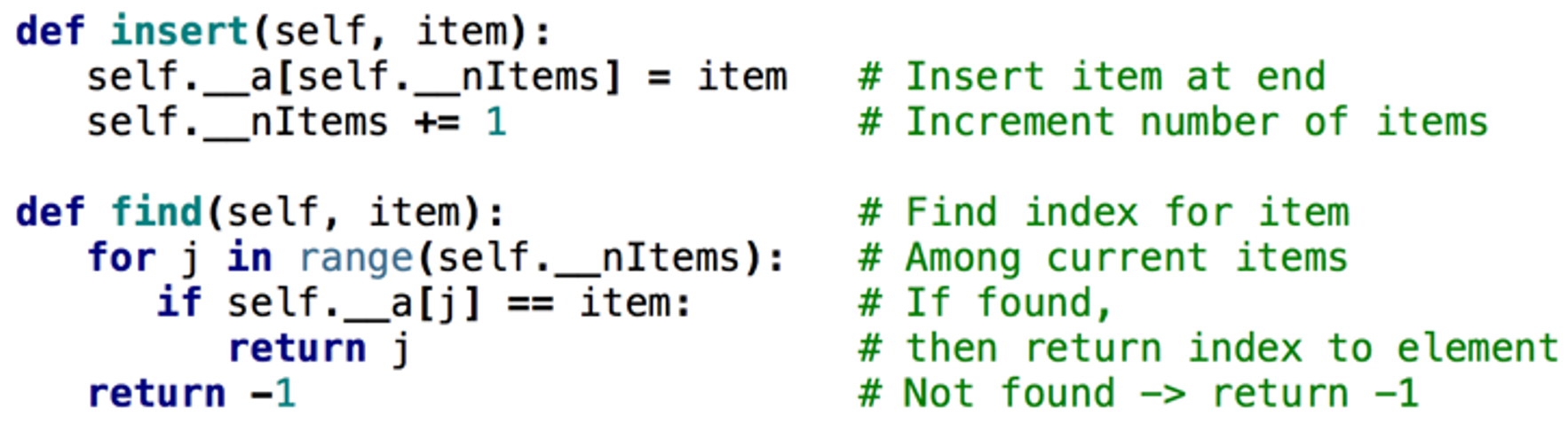
Unordered array: insert, find an item

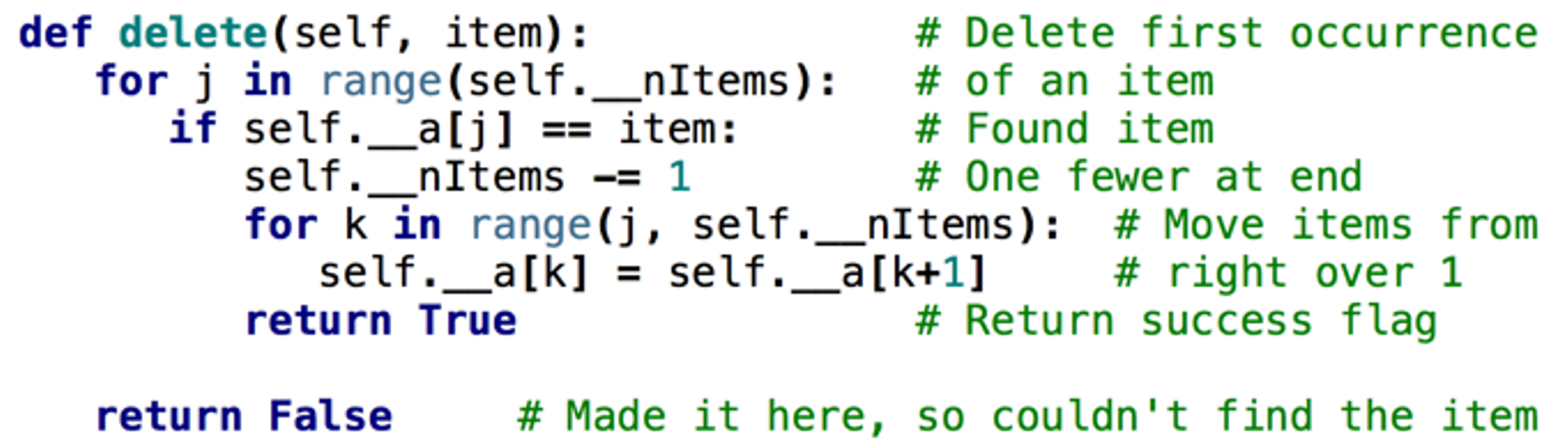
Unordered array: delete an item

Ordered Array class design

• Attributes (see in the next slide):
  • A list __a to store the elements of the array
  • A number __nItems to keep track of how many elements of a have been used so far.
• Methods:
  • Same as for Unordered Array, except insert and find
  • insert – insert an item at the correct place in array
  • find – more efficiently find where an item is (or where it should be) by taking advantage of the sorted order of the items in the OrderedArray

Ordered Array: Binary search to find

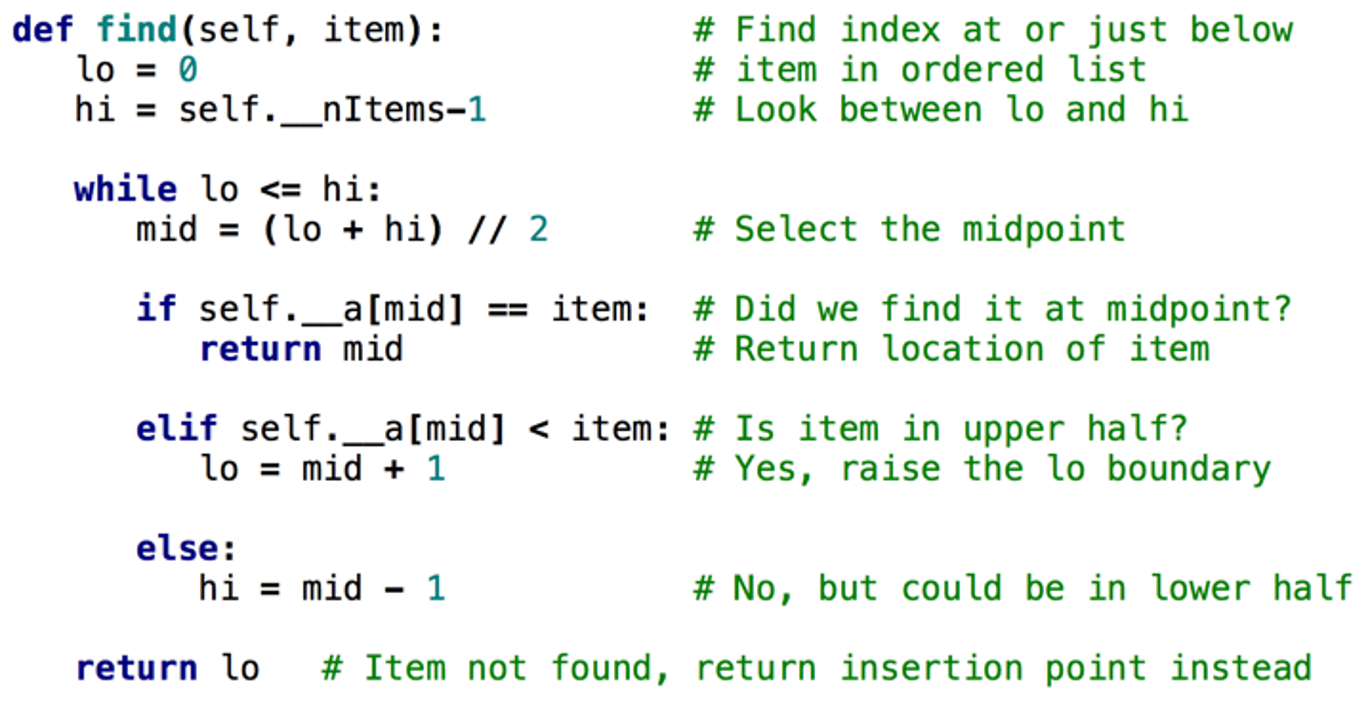
Ordered array: insert an item

Ordered array: delete an item

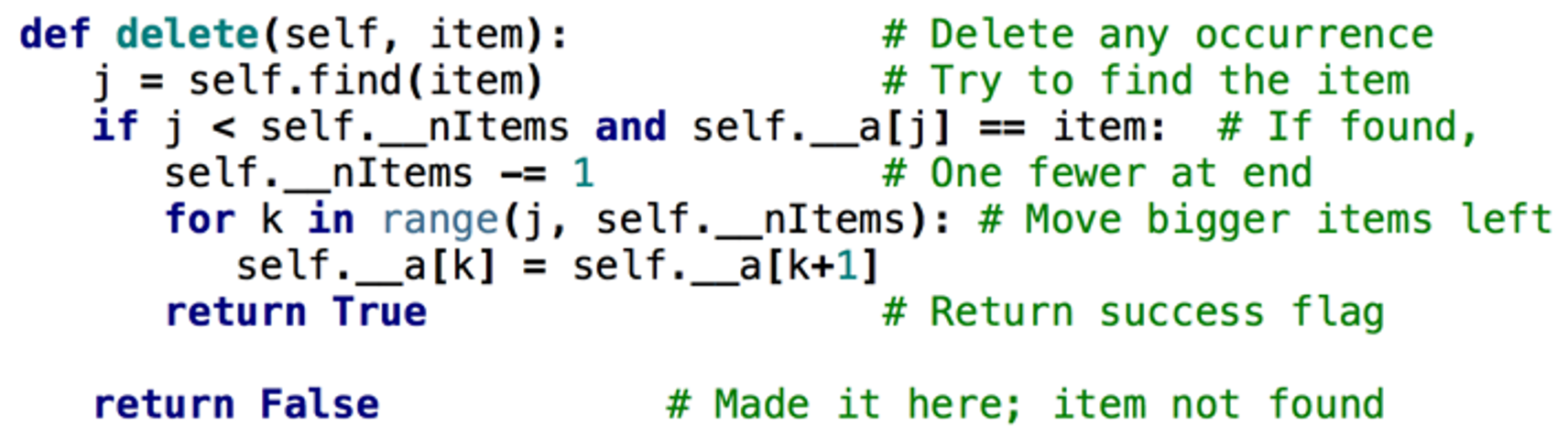
• Notice: if j == self.__nItems then the insertion point returned by self.find() is after the last element in the OrderedArray

More on the Traditional Arrays

Random Access and Contiguous Memory

• Array indexing is a random access operation:
  • The computer obtains the location of the ith item by performing a constant number of steps
  • No matter how large the array, it takes the same amount of time to access the first item as it does to access the last item
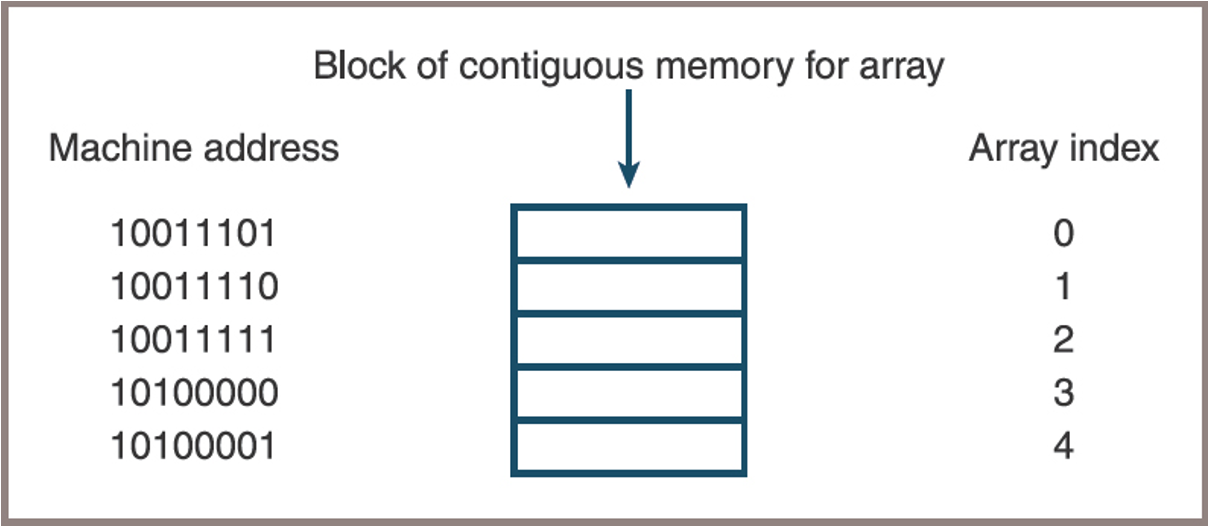
• The computer supports random access for arrays by allocating a block of contiguous memory cells for the array’s items (See in the next slide)

A block of contiguous memory

• This means you can compute the address of any element directly using its index, without scanning through the array.

  • Just adding the base address and the item’s offset
    • Base address is the address of the first item
    • Offset is index multiplied by the size_of_each_element

• Thus:

• address_of_element = base_address + (index * size_of_each_element)

• For Python, the size_of_each_element is 1

Block of Contiguous Memory

Revisiting Static vs. Dynamic Memory

• Arrays in older languages were static data structures
• Modern languages allow dynamic arrays:
  • Occupies a contiguous block of memory and supports random access
• The Python Array class allows the programmer to specify the length of a dynamic array during instantiation
• Ways that programmers can read just an array’s length
  • Create an array with a reasonable default size at program start-up
  • When the array cannot hold more data, create a new, larger array and transfer the data items from the old array
  • When the array seems to be wasting memory, decrease its length in a similar manner
• These adjustments happen automatically with a Python list

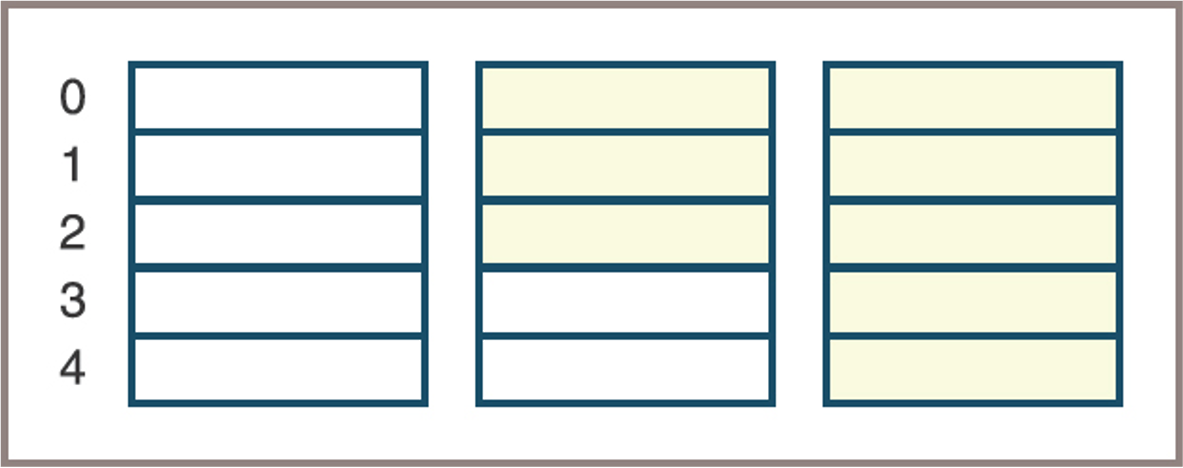
Physical Size and Logical Size

• Physical size of an array
  • Its total number of array cells or the number used to specify its capacity when the array is created
• Logical size of an array
  • The number of items in it that should be currently available to the application
• Logical and physical size tell you several things:
  • If the logical size is 0, the array is empty
  • Otherwise, at any given time, the index of the last item in the array is the logical size minus 1
  • If the logical size equals the physical size, there is no more room for data in the array

Physical Size and Logical Size

• Arrays with different logical sizes

Hidden Operations on Arrays

• This section shows the implementation of several operations on arrays that are hidden from users
• In these examples, assume the following data settings:

DEFAULT_CAPACITY = 5
logicalSize = 0
a = Array(DEFAULT_CAPACITY)

Increasing the Size of an Array

• The resizing process consists of three steps:
  • Create a new, larger array
  • Copy the data from the old array to the new array
  • Reset the old array variable to the new array object
• See Code:

if logicalSize == len(a):
    temp = Array(len(a) + 1)    # Create a new array
    for i in range(logicalSize):# Copy data from the old
        temp [i] = a[i]         # array to the new array
    a = temp                    # Reset the old array variable
                                # to the new array

Decreasing the Size of an Array

• The process of decreasing the size of an array is the inverse of increasing it
• Steps:
  • Create a new, smaller array
  • Copy the data from the old array to the new array
  • Reset the old array variable to the new array object
• See Code:

if logicalSize <= len(a) // 4 and len(a) >= DEFAULT_CAPACITY * 2:
    temp = Array(len(a) // 2)       # Create new array
    for i in range(logicalSize):    # Copy data from old array
        temp [i] = a [i]            # to new array
    a = temp                        # Reset old array variable to
                                    # new array

Inserting an Item into an Array That Grows

• In the case of an insertion, the programmer must do four things:
  • Check for available space before attempting an insertion and increase the physical size of the array, if necessary, as described earlier
  • Shift the items from the logical end of the array to the target index position down by one:
    • This process opens a hole for the new item at the target index
  • Assign the new item to the target index position
  • Increment the logical size by one

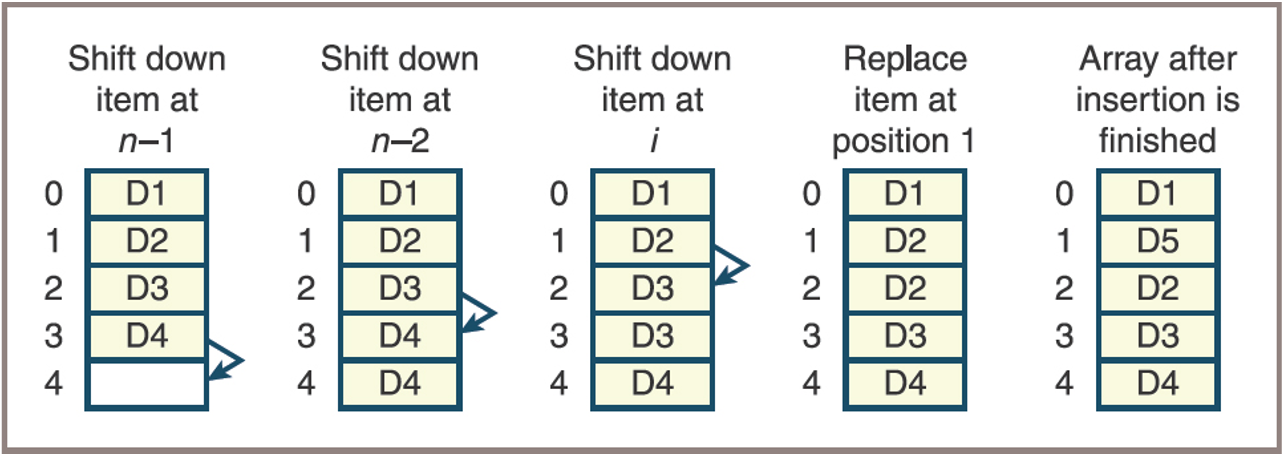
Inserting an Item into an Array That Grows

• Steps for the insertion of the item D5 at position 1

Inserting an Item into an Array That Grows

• Python code for the insertion operation:

# Increase physical size of array if necessary
# Shift items down by one position
for i in range(logicalSize, targetIndex, -1):
    a[i] = a[i - 1]
# Add new item and increment logical size
a[targetIndex] = newItem
logicalSize += 1

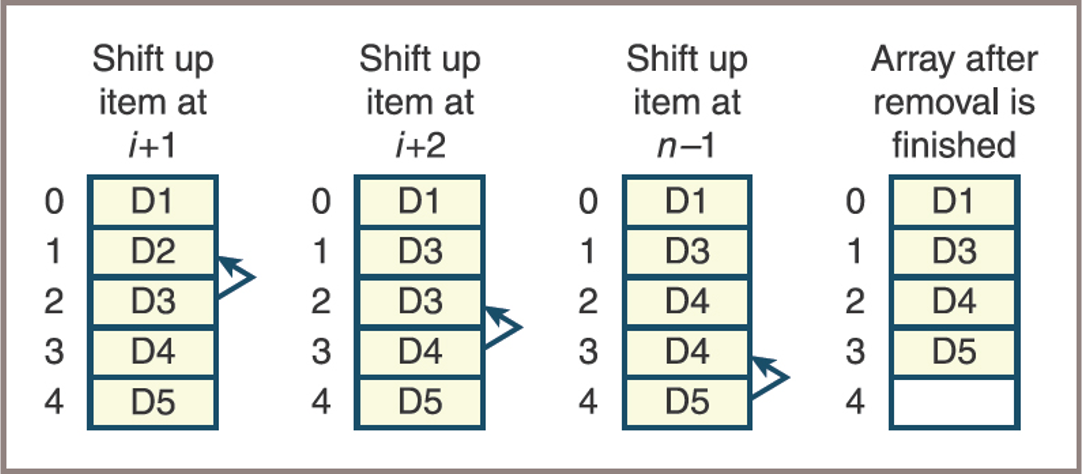
Removing an Item from an Array

• Steps for removing an item from an array
  • Shift the items from the one following the target index position to the logical end of the array up by one. This process closes the hole left by the removed item at the target index
  • Decrement the logical size by one
  • Check for wasted space and decrease the physical size of the array, if necessary

# Shift items up by one position
for i in range(targetIndex, logicalSize - 1):
    a[i] = a[i + 1]
# Decrement logical size
logicalSize -= 1
# Decrease size of array if necessary

Removing an Item from an Array

• Steps for the removal of an item at position 1

Analyzing performance: Unordered Array

• Insertion of 1 item at end of array: constant time
  • Amount of work (number of steps) does not depend on number of items in the array.
  • This is referred to as O(1) time
• Find or delete an item in an array of N items
  • On average, we expect to compare the key to N/2 array items before success, N items before failure.
  • Then we have to move on average N/2 items to the left
  • N/2 compares + N/2 moves
  • O(N) time

Analyzing performance: Ordered Array

• Find a key in an array of N items: how many iterations/comparisons?
  • log2(N), usually known as O(log N)
  • Why?
    • Every iteration of the binary search cuts the array of N elements in half
    • You can cut N in half log2(N) times until you get to 1
    • For example: 61, 30, 15, 7, 3, 1
• Insert or remove an item from an array of N items
  • Use binary search to find the location takes about log2(N)
  • But, we have to move on average N/2 items
  • Total operations are proportional to N/2 + log2(N)
  • Therefore, complexity is O(N) since N dominates the - log N term.

Summary Table:

• Array Operations and Running Times

Operation	Running Time
Access at ith position	O(1), best and worst cases
Replacement at ith position	O(1), best and worst cases
Insert at logical end	O(1), average case
Insert at ith position	O(n), average case
Remove from ith position	O(n), average case
Increase capacity	O(n), best and worst cases
Decrease capacity	O(n), best and worst cases
Remove from logical end	O(1), average case