Recursion Applications

Fred Agbo

2025-09-10

Announcements

• Welcome back!
• PS1 assignment is due today at 10pm
• First mini-project (MP1) is published today and due next week Wednesday
• Remember reading for next week is due on Wednesday

Real-Life Applications of Recursive Functions

Why Use Recursion in Real Life?

• Many problems are naturally recursive: they can be broken down into smaller, similar subproblems.
• Recursion is often used in:
  • Puzzles and games
  • Data structures (trees, graphs)
  • File system traversal
  • Algorithm design (divide and conquer)
  • Mathematical computations

Recursion in Puzzles and Games

• Recursion is widely used to solve puzzles and games that involve repeated, similar steps.
• Examples include:
  • Maze solving
  • Tic-Tac-Toe
  • Tower of Hanoi
  • Sudoku solvers

Developing a Recursive Puzzle Solver

• Steps to create a recursive puzzle solver:
  1. Identify the base case (when to stop recursion).
  2. Define the recursive case (how to break the problem into smaller parts).
  3. Ensure each recursive call moves closer to the base case.

Case Study 1: Maze Puzzle

• Problem: Find a path from the start to the end of a maze.
• Recursive approach:
  • At each position, try moving in all possible directions.
  • Mark visited positions to avoid cycles.
  • If the end is reached, return success.
  • If all paths are blocked, backtrack.

Walk through a Maze Example in Python

# Recursive function to solve a maze
def solve_maze(maze, x, y, path):
    # Base case: reached the end
    if maze[x][y] == 'E':
        path.append((x, y))
        return True
    # Mark current cell as visited
    maze[x][y] = '#'
    # Possible moves: right, down, left, up
    moves = [(0,1), (1,0), (0,-1), (-1,0)]
    for dx, dy in moves:
        nx, ny = x + dx, y + dy
        if 0 <= nx < len(maze) and 0 <= ny < len(maze[0]) and maze[nx][ny] in (' ', 'E'):
            if solve_maze(maze, nx, ny, path):
                path.append((x, y))
                return True
    return False

Let’s walk through your solvemaze function step by step, focusing on how recursion is used to solve the maze.

1. Function Definition
   • maze: 2D list representing the maze.
   • x, y: Current position in the maze.
   • path: List to store the path taken.
2. Base Case: Reaching the End
   • If the current cell is “E” (the exit), add the position to path and return True.
   • This stops the recursion and signals that a solution has been found.
3. Marking the Cell as Visited
   • Marks the current cell as visited to avoid revisiting and infinite loops.
4. Possible Moves -Represents moving right, down, up, and left.
5. Recursion: Exploring Neighbors
   • For each direction, calculate the new position (nx, ny).
   • Check if the new position is inside the maze and is either an empty space ’ ’ or the exit ‘E’.
   • Recursively call solvemaze for the new position.
   • If a path is found (True), add the current position to path and return True.
6. No Path Found
   • If none of the moves lead to the exit, return False (backtrack).

Walk through a Maze Example in Python

# Example usage:
maze = [
    ['S', ' ', ' ', '#', ' ', ' ', ' '],
    ['#', '#', ' ', '#', ' ', '#', ' '],
    [' ', ' ', ' ', ' ', ' ', '#', ' '],
    [' ', '#', '#', '#', ' ', '#', ' '],
    [' ', ' ', ' ', '#', ' ', ' ', 'E']
]
path = []
solve_maze(maze, 0, 0, path)
print("Path to exit:", path[::-1])

7. Maze Setup and Function Call
   • Defines the maze.
   • Calls solvemaze starting at (0, 0) (top-left).
   • Prints the path in reverse order (from start to end).
8. How Recursion Works Here
   • The function keeps calling itself for each possible move.
   • If it reaches the exit, it returns True and builds the path.
   • If it hits a wall or a visited cell, it returns False and backtracks.
   • This process continues until all possibilities are explored.

Case Study 2: Tic-Tac_Toe

• Tic-Tac-Toe is a 3x3 grid game for two players (X and O).
• The goal is to get three of your marks in a row (horizontally, vertically, or diagonally).

Your Approach

• Step 1: Represent the Game State
  • Use a 2D array or list of lists to represent the 3x3 board.
  • Each cell holds ‘X’, ‘O’, or empty value.
• Step 2: Define the Base Case (End Conditions)
  • Recursion ends if:
  • There is a winner (three in a row).
  • The board is full (draw).
  • Write a function to detect a winner or draw on the current board.

Your Approach

• Step 3: Define the Recursive Case
  • For the current player’s turn:
  • Generate all possible next moves (empty cells).
  • For each possible move:
    • Make the move.
    • Recursively call the function to evaluate the opponent’s best response.
      • Minimax Algorithm
  • Maximize the current player’s outcome while minimizing the opponent’s chance of winning.
• Aggregate results to decide the best move for the current player.

Tic-Tac-Toe Walkthrough Pseudocode

function minimax(board, player):
    if winner(board) or board full:
        return score of board (1 for win, -1 for loss, 0 for draw)
    
    if player is maximizing:
        bestScore = -∞
        for each valid move:
            make move
            score = minimax(board, opponent)
            undo move
            bestScore = max(score, bestScore)
        return bestScore
    else: # minimizing player
        bestScore = +∞
        for each valid move:
            make move
            score = minimax(board, opponent)
            undo move
            bestScore = min(score, bestScore)
        return bestScore

Case Study 3: Tower of Hanoi

• Classic puzzle involving three rods/spindles/columns, and a number of disks of different sizes.

• Also known as the Tower of Brahma or Lucas’s Tower for Édouard Lucas

• All the disks start out on one rod, stacked in order of diameter, which gives the appearance of a tower

ToH Rules

• Goal: Move all disks from the source rod to the destination rod, following these rules:
  1. Only one disk can be moved at a time.
  2. Each move consists of taking the upper disk from one rod and placing it on another rod.
  3. No disk may be placed on top of a smaller disk.

The Legend Behind Tower of Hanoi

• The Tower of Hanoi puzzle is inspired by a legend:
  • In a temple, monks were tasked with moving 64 golden disks from one rod to another, following the puzzle’s rules.
  • According to the legend, when the monks complete the puzzle, the world will end.
  • The puzzle demonstrates the power (and limits) of recursion:
    • The minimum number of moves required is (2ⁿ - 1), where n is the number of disks.
    • For 64 disks, this is an astronomically large number—making the task practically impossible!

How to solve ToH

• The problem can be solved recursively:
  • Move n-1 disks from source to auxiliary rod.
  • Move the largest disk to destination rod.
  • Move n-1 disks from auxiliary to destination rod.

ToH with disk (n)=3

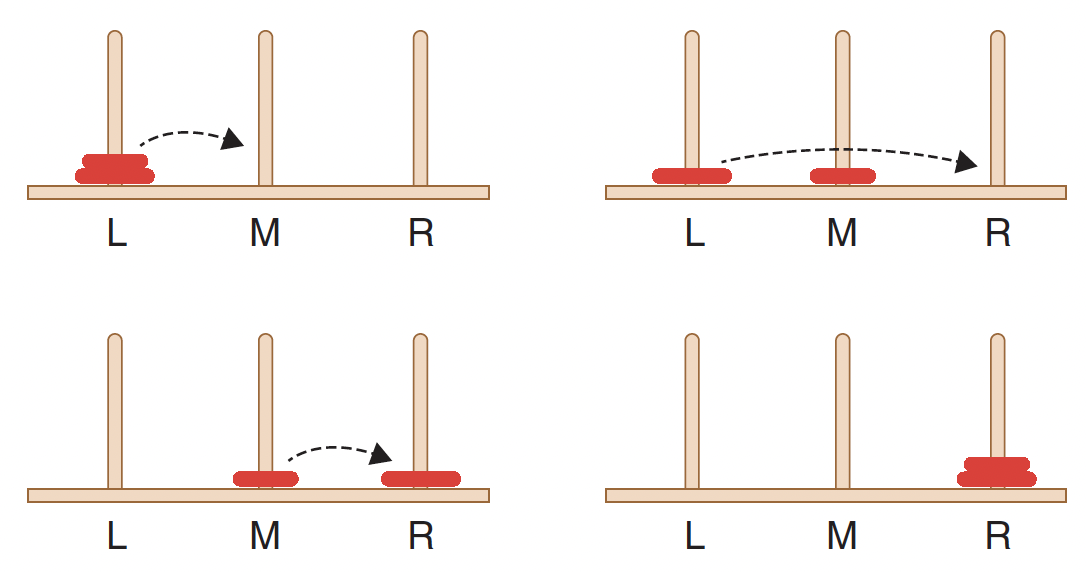
Visualize ToH Solutions & play more!

• Link to the online visualization

ToH Python Implementation

# Pythonic function-based ToH 
def create_tower_of_hanoi(n_disks=3):
    stacks = [[] for _ in range(3)]
    labels = ['L', 'M', 'R']
    # Initialize first spindle with disks in descending order
    stacks[0] = list(range(n_disks, 0, -1))
    return stacks, labels

def reset_tower(stacks, n_disks):
    for spindle in range(3):
        stacks[spindle] = []
    stacks[0] = list(range(n_disks, 0, -1))

def label(labels, spindle):
    return labels[spindle]
# Lenght of each rod = number of disk on a spindle
def height(stacks, spindle):
    return len(stacks[spindle])

def top_disk(stacks, spindle):
    if stacks[spindle]:
        return stacks[spindle][-1]
    return None
#Create the tower
def tower_str(stacks, labels):
    result = ""
    for spindle in range(3):
        if result:
            result += "\n"
        result += f"{labels[spindle]}: {stacks[spindle]}"
    return result

## ToH movement
def move(stacks, labels, source, to, show=False):
    if not stacks[source]:
        raise Exception("Cannot move from empty spindle " + labels[source])
    if stacks[to] and stacks[source][-1] > stacks[to][-1]:
        raise Exception(
            "Cannot move disk " + str(stacks[source][-1]) +
            " on top of disk " + str(stacks[to][-1])
        )
    disk = stacks[source].pop()
    stacks[to].append(disk)
    if show:
        print('Move disk', disk, 'from spindle', labels[source], 'to', labels[to])

## Recursive function 'Solve'
def solve(stacks, labels, n_disks=None, start=0, goal=2, spare=1, show=False, total_disks=None):
    if n_disks is None:
        n_disks = len(stacks[start])
    if total_disks is None:
        total_disks = n_disks
    if n_disks <= 0:
        return
    if len(stacks[start]) < n_disks:
        raise Exception(
            "Not enough disks (" + str(n_disks) +
            ") on starting spindle " + labels[start]
        )
    ## Recursive call
    solve(stacks, labels, n_disks - 1, start, spare, goal, show, total_disks)
    move(stacks, labels, start, goal, show)
    if show:
        print(tower_str(stacks, labels))
    solve(stacks, labels, n_disks - 1, spare, goal, start, show, total_disks)
    if n_disks == total_disks and show:
        print("Puzzle complete")

# Example usage:
n_disks = 3
stacks, labels = create_tower_of_hanoi(n_disks)
print(tower_str(stacks, labels))
solve(stacks, labels, show=True)

OOP Preview

Use Classes Before the Bag Mini-Project?

• Object-Oriented Programming (OOP) lets you model real-world entities as objects.
• For the upcoming Bag mini-project, you’ll use classes to:
  • Represent a Bag as an object with attributes (like items) and methods (like add, remove).
  • Encapsulate logic and state, making your code modular and reusable.
  • Easily extend functionality (e.g., support for different types of Bags).
• Example class structure:

Introducing Object-Oriented Programming (OOP) in Python

• OOP is a programming paradigm based on the concept of “objects”.
• Objects are instances of classes, which can contain data (attributes) and functions (methods).
• Organizes code for complex data structures.
• Makes code reusable and easier to maintain.
• Models real-world entities.

Example: Real World Objects

• For example, a Car object could have attributes like color and speed, and methods like drive() or brake().
• Similarly, a Student object might store a name and grade, and have methods to enroll in courses or update grades.

Example: Defining Student Class

class Student:
    def __init__(self, name, grade):
        self.name = name
        self.grade = grade

    def enroll(self, course):
        print(f"{self.name} enrolled in {course}")

    def update_grade(self, new_grade):
        self.grade = new_grade
        print(f"{self.name}'s grade updated to {self.grade}")

    def display_info(self):
        print(f"Name: {self.name}, Grade: {self.grade}")

# Example usage:
student1 = Student("Alice", "A")
student1.enroll("Math")
student1.update_grade("A+")
student1.display_info()

Example: Defining Car Class

class Car(object):
    def __init__(self, color, speed):
        self.color = color
        self.speed = speed

    def drive(self):
        print(f"The {self.color} car is driving at {self.speed} mph.")

    def brake(self):
        print(f"The {self.color} car is braking.")

# Example usage:
car1 = Car("red", 60)
car1.drive()
car1.brake()

Next week!

• Reading for next week Arrays:
  • Fundamentals of Python Data Structures (FDS) - Lambert: ,
    • Chapters 4
  • Data Structures & Algorithms in Python (DS&A) - John et al.:
    • Chapter 2 & 5