GRAPHS IMPLEMENTATION
Fred Agbo
2025-11-24
Developing a Graph Collection
Announcements
- Mini Project #3 is due today.
- Grading of PS5 was completed. Let me know if you have any concern about my comments.
- Last day in class will be Wednesday December 3
- Make arrangement to be in class on December 1 & 3
- Checkout the
Course Evaluation Menu/link on your Canvas - I need volunteers to participate in my study
- Evaluation of a VR prototype for STEM education
- WIll last for about 15 to 20 minutes to complete
Developing a Graph Collection
- To develop a graph collection, consider the following:
- The requirements of users
- The mathematical nature of graphs
- The commonly used representations, adjacency matrix, and adjacency list
- Users should be able to
- Insert and remove vertices
- Insert or remove an edge
- Retrieve all the vertices and edges
- Choose between directed and undirected graphs and between an adjacency matrix representation and an adjacency list representation
Example Use of the Graph Collection
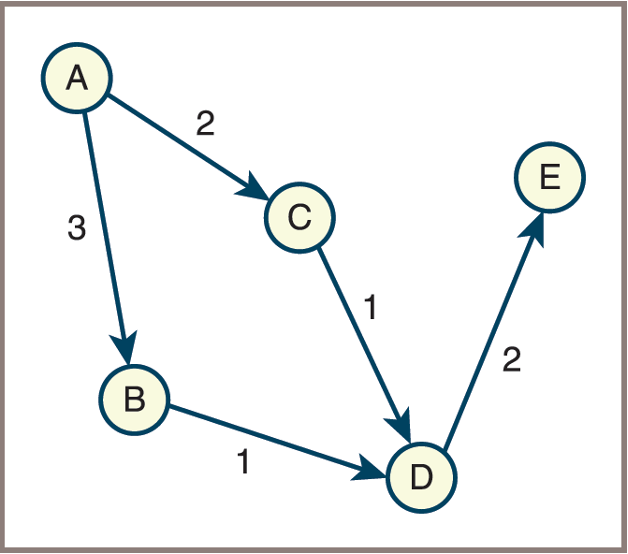
- Consider constructing this weighted graph:
![]()
- Code
from graph import LinkedDirectedGraph
g = LinkedDirectedGraph()
# Insert vertices
g.addVertex("A")
g.addVertex("B")
g.addVertex("C")
g.addVertex("D")
g.addVertex("E")
# Insert weighted edges
g.addEdge("A", "B", 3)
g.addEdge("A", "C", 2)
g.addEdge("B", "D", 1)
g.addEdge("C", "D", 1)
g.addEdge("D", "E", 2)
print(g)- Output:
5 Vertices: A C B E D5 Edges: A>B:3 A>C:2 B>D:1 C>D:1 D>E:2
Example Use of the Graph Collection
The next code segment displays the neighboring vertices and the incident edges of the vertex labeled
Ain this example graph:Neighboring vertices of
A
print("Neighboring vertices of A:")
for vertex in g.neighboringVertices("A"):
print(vertex)
# Output:
Neighboring vertices of A:
B
C- Incident edges of the vertex labeled
A
Graph Implementation
- Paths of least resistance in the graph implementation
- You make a graph class a subclass of
AbstractCollection - You make a graph’s size equal to its number of vertices
- The
addmethod adds a vertex with the given label to a graph - You allow a graph’s iterator to visit its vertices
- You make a graph class a subclass of
- Consequences
- The
lenfunction returns the number of the graph’s vertices - The graph constructor’s source collection contains the labels of the new graph’s vertices
- The
forloop visits the graph’s vertices - The
inoperator returnsTrueif the graph contains a given vertex - The
==operator compares vertices in the two graph operands - The
+operator creates a new graph that contains the vertices of its two operands
- The
Graph Implementation: Classess & Methods
- The graph implementation described here uses a linked structure.
- Each vertex and edge is represented as an object (node) that contains references (links) to other vertices and edges.
- This approach allows efficient traversal and modification of the graph, as each vertex maintains links to its adjacent edges and vertices.
- Three Classes to model
- Class
LinkedDirectedGraph - Class
LinkedVertex - Class
LinkedEdge
- Class
Class LinkedDirectedGraph(1/2)
The LinkedDirectedGraph class typically provides the following methods:
| Method | What It Does |
|---|---|
| Graph Creation | |
g = LinkedDirectedGraph(sourceCollection=None) |
Creates a new directed graph using an adjacency list. Optionally adds vertices from a collection of labels. |
| Clearing, Size, and String Representation | |
g.clear() |
Removes all vertices from the graph. |
g.clearEdgeMarks() |
Clears all edge marks. |
g.clearVertexMarks() |
Clears all vertex marks. |
g.isEmpty() |
Returns True if the graph contains no vertices. |
g.sizeEdges() |
Returns the number of edges in the graph. |
g.sizeVertices() |
Returns the number of vertices in the graph. |
g.__str__() |
Returns a string representation of the graph. |
| Vertex-Related Methods | |
g.containsVertex(label) |
Returns True if the graph contains a vertex with the specified label. |
g.addVertex(label) |
Adds a vertex with the specified label. |
g.getVertex(label) |
Returns the vertex with the specified label, or None if not found. |
g.removeVertex(label) |
Removes and returns the vertex with the specified label, or None if not found. |
Class LinkedDirectedGraph (2/2)
| Method | What It Does |
|---|---|
| Edge-Related Methods | |
g.containsEdge(fromLabel, toLabel) |
Returns True if an edge exists from fromLabel to toLabel. |
g.addEdge(fromLabel, toLabel, weight=None) |
Adds an edge with the specified weight between the given vertices. |
g.getEdge(fromLabel, toLabel) |
Returns the edge between the specified vertices, or None if not found. |
g.removeEdge(fromLabel, toLabel) |
Removes the edge and returns True if successful, else False. |
| Iterators | |
g.edges() |
Returns an iterator over the edges in the graph. |
g.getVertices() |
Returns an iterator over the vertices in the graph. |
g.incidentEdges(label) |
Returns an iterator over the incident edges of the vertex with the given label. |
g.neighboringVertices(label) |
Returns an iterator over the neighboring vertices of the given vertex. |
The Class LinkedDirectedGraph ADT
The implementation of
LinkedDirectedGraphmaintains adictionarywhose keys arelabelsand whose values are the correspondingverticesCode for the class header and constructor:
class LinkedDirectedGraph(AbstractCollection):
def __init__(self, sourceCollection = None):
self.edgeCount = 0
self.vertices = dict() # Dictionary of vertices {}
AbstractCollection.__init__(self, sourceCollection)- Notice that the
LinkedDirectedGraphclass is inheritingAbstractCollectionclass
The Class LinkedDirectedGraph
- Methods
- Code for adding, accessing, and removing an edge:
def addEdge(self, fromLabel, toLabel, weight):
"""Connects the vertices with an edge with the given weight."""
fromVertex = self.getVertex(fromLabel)
toVertex = self.getVertex(toLabel)
fromVertex.addEdgeTo(toVertex, weight)
self.edgeCount += 1
def getEdge(self, fromLabel, toLabel):
"""Returns the edge connecting the two vertices, or None if
no edge exists."""
fromVertex = self.getVertex(fromLabel)
toVertex = self.getVertex(toLabel)
return fromVertex.getEdgeTo(toVertex)
def removeEdge(self, fromLabel, toLabel):
"""Returns True if the edge was removed, or False otherwise."""
fromVertex = self.getVertex(fromLabel)
toVertex = self.getVertex(toLabel)
edgeRemovedFlg = fromVertex.removeEdgeTo(toVertex)
if edgeRemovedFlg:
self.edgeCount -= 1
return edgeRemovedFlgThe Class LinkedVertex
- The methods in the class
LinkedVertex
| Method | What It Does |
|---|---|
LinkedVertex(label) |
Creates a vertex with the specified label. The vertex is initially unmarked. |
clearMark() |
Unmarks the vertex. |
setMark() |
Marks the vertex. |
isMarked() |
Returns True if the vertex is marked, or False otherwise. |
getLabel() |
Returns the label of the vertex. |
setLabel(label, g) |
Changes the label of the vertex in graph g to label. |
addEdgeTo(toVertex, weight) |
Adds an edge with the given weight from this vertex to toVertex. |
getEdgeTo(toVertex) |
Returns the edge from this vertex to toVertex, or None if the edge does not exist. |
incidentEdges() |
Returns an iterator over the incident edges of the vertex. |
neighboringVertices() |
Returns an iterator over the neighboring vertices of the vertex. |
__str__() |
Returns a string representation of the vertex. |
__eq__(anyObject) |
Returns True if anyObject is a vertex and the two labels are the same. |
The Class LinkedVertex: Structure
- Code segment here shows the constructor and the method setLabel:
The Class LinkedEdge
- The methods in the class
LinkedEdge
| Method | What It Does |
|---|---|
LinkedEdge(fromVertex, toVertex, weight=None) |
Creates an edge with the specified vertices and weight. It is initially unmarked. |
clearMark() |
Unmarks the edge. |
setMark() |
Marks the edge. |
isMarked() |
Returns True if the edge is marked, or False otherwise. |
getWeight() |
Returns the weight of the edge. |
setWeight(weight) |
Sets the edge’s weight to the specified weight. |
getOtherVertex(vertex) |
Returns the edge’s other vertex. |
getToVertex() |
Returns the edge’s destination vertex. |
__str__() |
Returns the string representation of the edge. |
__eq__(anyObject) |
Returns True if anyObject is an edge and the two edges are connected to the same vertices and have the same weight. |
The Class LinkedEdge
- An edge maintains references to its two vertices, its weight, and a mark
- Although the weight can be any object labeling the edge,
- The weight is often a number or some other comparable value
- Two edges are considered equal if they have the same vertices and weight
The Class LinkedEdge: Structure
- Code for the constructor and the
_eq_method:
class LinkedEdge(object):
def __init__(self, fromVertex, toVertex, weight = None):
self.vertex1 = fromVertex
self.vertex2 = toVertex
self.weight = weight
self.mark = False
def __eq__(self, other):
"""Two edges are equal if they connect
the same vertices."""
if self is other: return True
if type(self) != type(other): return False
return self.vertex1 == other.vertex1 and \
self.vertex2 == other.vertex2 and \
self.weight == other.weightPS6: Homework
- Case Study: Testing Graph Algorithms
- In Foundamentals of Python Data Structures (2nd Ed.) by Lambert
- Chapter 12
- Pages 391 to 397
- In Foundamentals of Python Data Structures (2nd Ed.) by Lambert
- Download starter code here
Instructions
- This case study develops a data model and user interface that allow the programmer to create graphs and use them to test graph algorithms.
- Use the ADT of graph implementation discussed in the class today plus other modules provided in the case study to:
- Write a program that allows the user to test some graph-processing algorithms (see the case study for detailed implementation strategies including starter codes)
Tasks
Complete the classes in the case study and test the operations to input a graph and display it.
Complete the function
spanTreein the case study and test it thoroughly.Complete the function
shortestPathsin the case study and test it thoroughly
Homework Submission
- This home work will be discussed in the class on Monday December 1
- Each student will take turn to
show-&-tellby demonstrating their solution
- Each student will take turn to