GRAPHS TRAVERSALS 2

Fred Agbo

2025-11-19

Announcements

• Mini Project #3 is due next week Monday.
• Grading of PS5 is ongoing

Class Worksheet Activity

Review of Mini Project 3

Recall Minimum Spanning Tree

• A Minimum Spanning Tree (MST) is a spanning tree of a weighted, connected, undirected graph with the smallest possible total edge weight.
• MSTs are used in network design, clustering, and other optimization problems.

Recall Minimum Spanning Tree

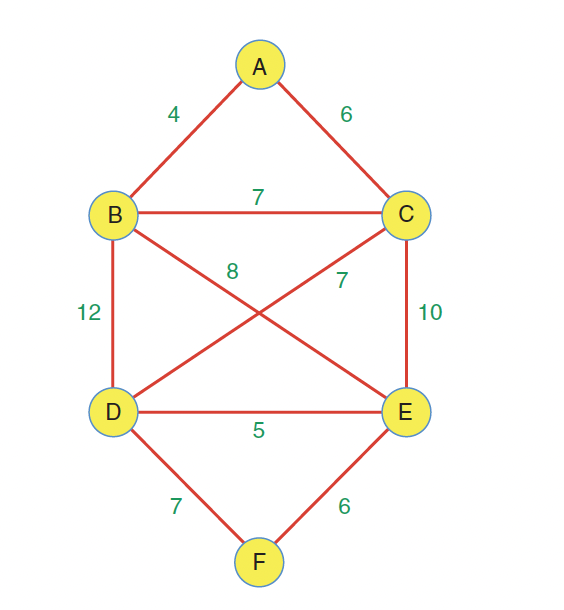
• Here is a weighted graph with six vertices. Each edge has a weight, shown by a number alongside the edge.

• How can you pick a subgraph that minimizes the cost of connecting vertices into a network?

Recall Minimum Spanning Tree

• The answer is to calculate a minimum spanning tree.
• It will have five edges (one fewer than the number of vertices), it will connect all six vertices
• It will minimize the total cost of the links.

Recall Minimum Spanning Tree

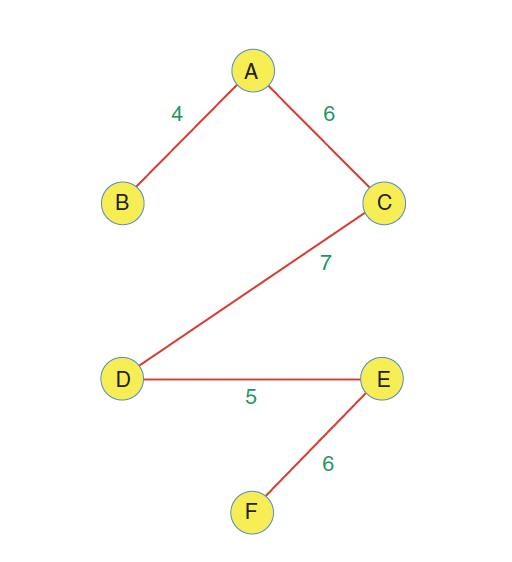
• The MST for the graph above

• The minimum spanning tree consists of the edges AB, AC, CD, DE, and EF, for a total edge weight of 28

• The order in which the edges are specified is unimportant.

The Shortest-Path Problem

• It is often useful to determine the shortest path between two vertices in a graph
• The single-source shortest path problem asks for a solution that contains the shortest paths from a given vertex to all other vertices:
  • Solution by Dijkstra: \(O(N^2)\)
• Another problem, all-pairs shortest path problem, asks for the set of all the shortest paths in a graph:
  • Solution by Floyd: \(O(N^3)\)

Dijkstra’s Algorithm

• Dijkstra’s algorithm finds the shortest paths from a single source vertex to all other vertices in a weighted graph with non-negative edge weights.
• The algorithm maintains a set of visited vertices and a distance stored in results as 2D array.
• At each step, it selects the unvisited vertex with the smallest known distance, updates the distances to its neighbors, and marks it as visited.
• The algorithm uses a temporary list, included, of N Booleans
  • To track whether or not a given vertex has been included in the set of vertices for which you already have determined the shortest path
• The algorithm consists of two major steps:
  • An initialization step
  • A computation step

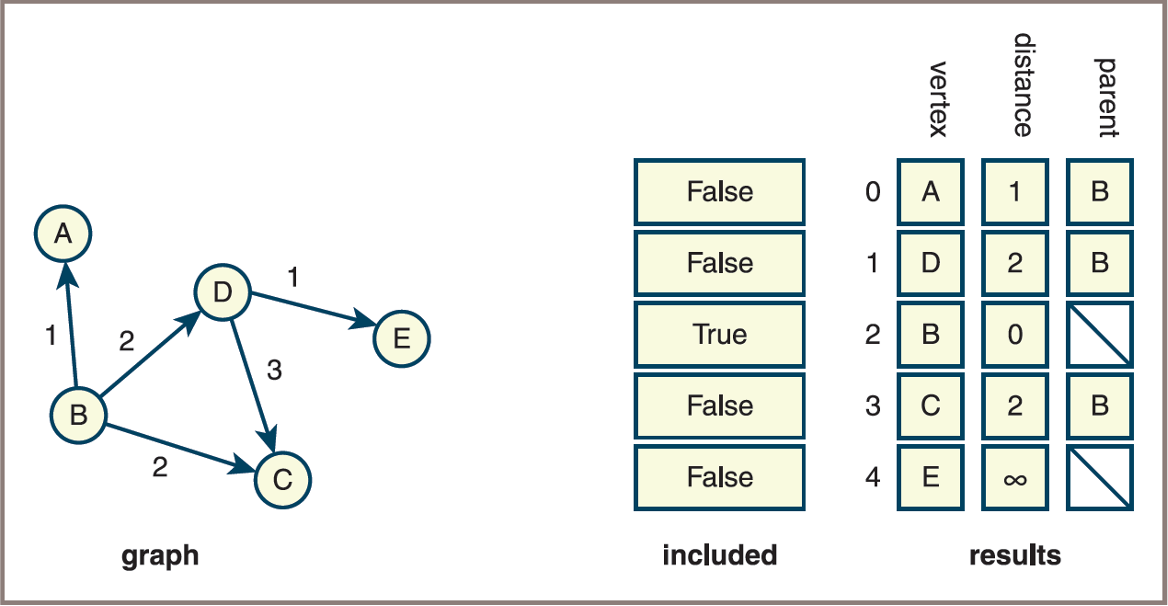
Dijkstra’s Algorithm: Initialization Step

• Initialize all the columns in the results grid and all the cells in the included list according to the following algorithm:

for each vertex in the graph
    Store vertex in the current row of the results grid
    If vertex = source vertex
        Set the row’s distance cell to 0
        Set the row’s parent cell to undefined
        Set included[row] to True
    Else if there is an edge from source vertex to vertex
        Set the row’s distance cell to the edge’s weight
        Set the row’s parent cell to source vertex
        Set included[row] to False
    Else
        Set the row’s distance cell to infinity
        Set the row’s parent cell to undefined
        Set included[row] to False
    Go to the next row in the results grid

Dijkstra’s Algorithm: Initialization Step

• A graph and the initial state of the data structures used to compute the shortest paths from a given vertex

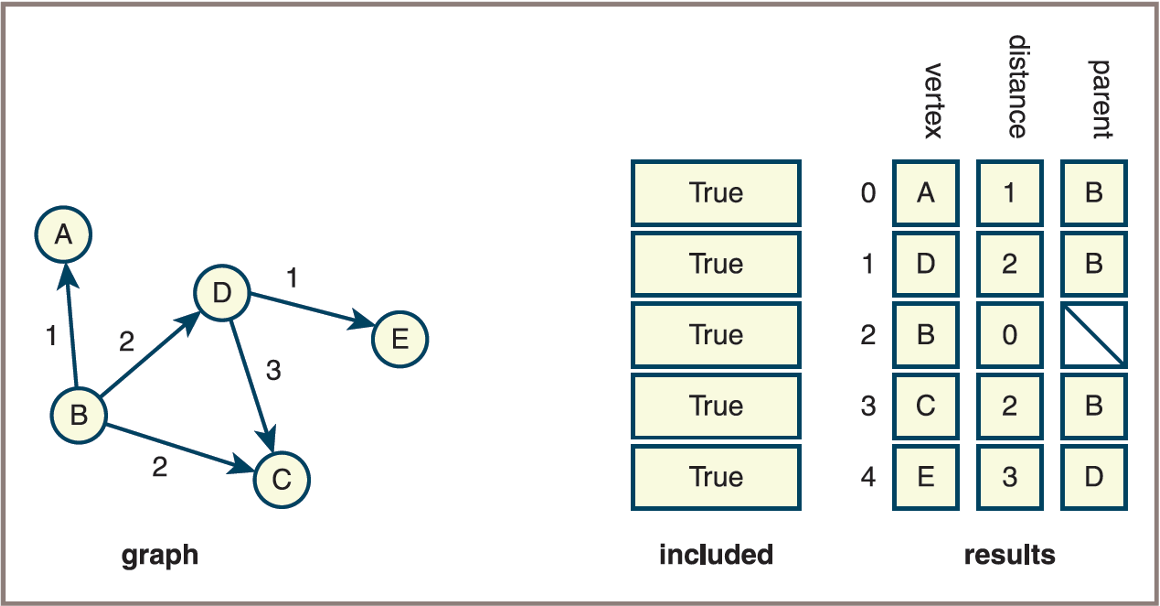
Dijkstra’s Algorithm: Computation Step

• Dijkstra’s algorithm finds the shortest path from the source to a vertex, marks this vertex’s cell in the included list, and continues this process until all these cells are marked:

Do
    Find the vertex F that is not yet included and has the minimal distance in the results grid
    Mark F as included
    For each other vertex T not included
        If there is an edge from F to T
            Set new distance to F’s distance + edge’s weight
            If new distance < T’s distance in the results grid
                Set T’s distance to new distance
                Set T’s parent in the results grid to F
While at least one vertex is not included

Dijkstra’s Algorithm: Computation Step

• A graph and the final state of the data structures used to compute the shortest paths from a given vertex

Dijkstra’s Algorithm: Analysis

• The initialization step must process every vertex
  • So it is O(n)
• The outer loop of the computation step also iterates through every vertex
• The inner loop of this step iterates through every vertex not included thus far
• The overall behavior of the computation step resembles that of other \(O(N^2)\) algorithms, so Dijkstra’s algorithm is \(O(N^2)\)

Floyd’s Algorithm

• Floyd’s algorithm (Floyd-Warshall) solves the all-pairs shortest path problem for a weighted graph.
• It works for both directed and undirected graphs, and can handle negative edge weights (but not negative cycles).
• The algorithm uses a 2D matrix to store shortest distances between every pair of vertices.
• It repeatedly updates the matrix by considering each vertex as an intermediate point.

Floyd’s Algorithm

• For each vertex v in a graph, the algorithm finds the shortest path from vertex v to any other vertex w that is reachable from v

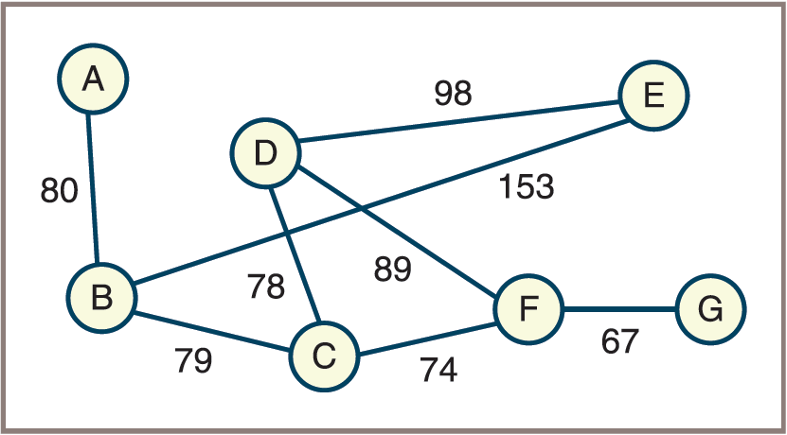
• Consider the weighted graph in this Figure

Floyd’s Algorithm: In a preprocessing step

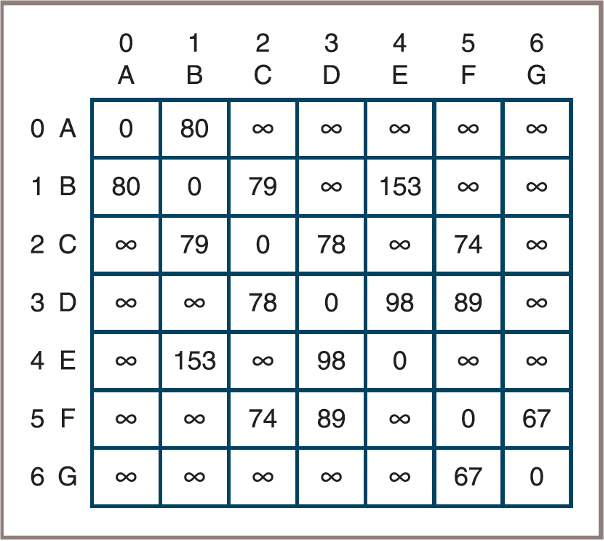
• Using the figure above, you will build an initial distance matrix whose cells contain the weights on the edges that connect each vertex with its neighbors

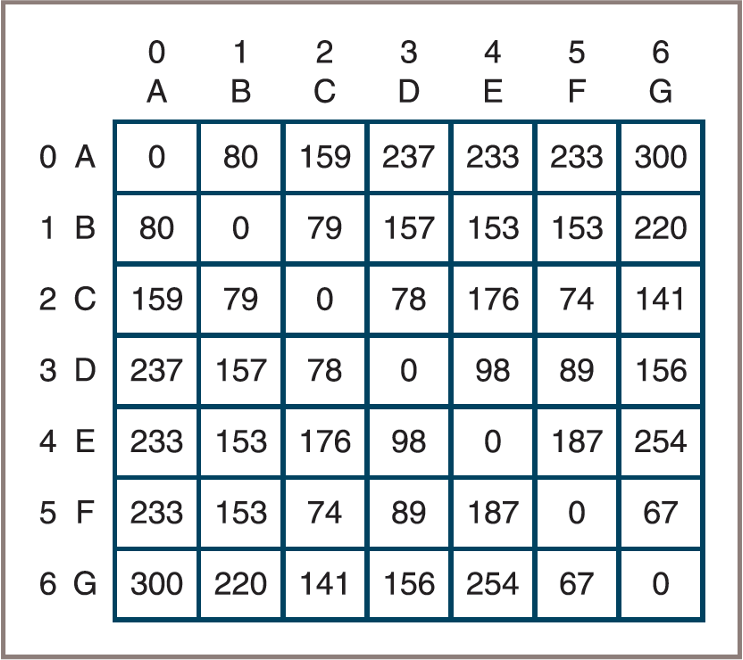
Floyd’s Algorithm: Computational step

• Using the figure above, here is the modified distance matrix:

Floyd’s Algorithm

Pseudocode:

for i from 0 to n - 1
    for r from 0 to n - 1
        for c from 0 to n - 1
            matrix[r][c] = min(matrix[r][c],
                              matrix[r][i] + matrix[i][c])

Floyd’s Algorithm: Analysis

• The initialization step to create the distance matrix from the graph is \(O(N^2)\)
  • This matrix is actually the same as an adjacency matrix representation of the given graph
• Because Floyd’s algorithm includes three nested loops over N vertices, the algorithm itself is \(O(N^3)\)
• The overall running time of the process is bounded by \(O(N^3)\)