GRAPHS TRAVERSALS

Fred Agbo

2025-11-17

Announcements

Mini Project #3 is due next week Monday.
Grading of PS5 is ongoing

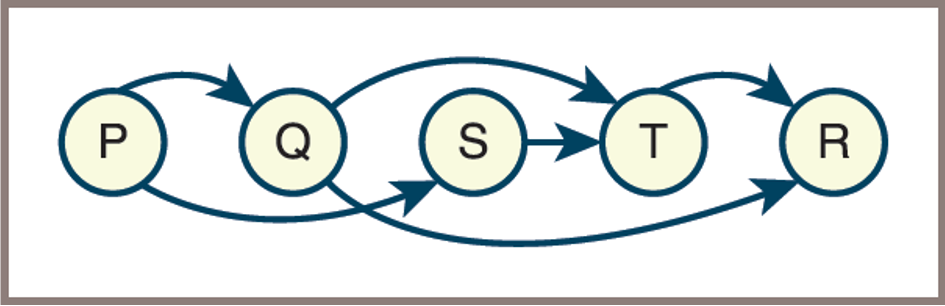
Class Worksheet Activity: 1

Describing Types of Graph Traversals

Important graph-processing operations include the following:
- Finding the shortest path to a given item in a graph
- Finding all the items to which a given item is connected by paths
- Traversing all the items in a graph

A Generic Traversal Algorithm

Graph traversal algorithms start at a given vertex and move outward to explore paths to neighboring vertices
We’ll use a generic function that performs a graph traversal, which starts at an arbitrary vertex startVertex
Pseudocode:

traverseFromVertex(graph, startVertex, process):
    mark all vertices in the graph as unvisited
    add the startVertex to an empty collection
    while the collection is not empty:
        pop a vertex from the collection
        if the vertex has not been visited:
            mark the vertex as visited
            process(vertex)
            add all adjacent unvisited vertices to the collection

A Generic Traversal Algorithm

for a graph that contains N vertices, the following applies:
- All vertices reachable from startVertex are processed exactly once
- Determining all the vertices adjacent to a given vertex is straightforward.
  - When an adjacency matrix is used, you iterate across the row corresponding to the vertex
  - When an adjacency list is used, you traverse the vertex’s linked list.

Common Order of Graph Traversals

Two common orders in which vertices can be visited during a graph traversal:
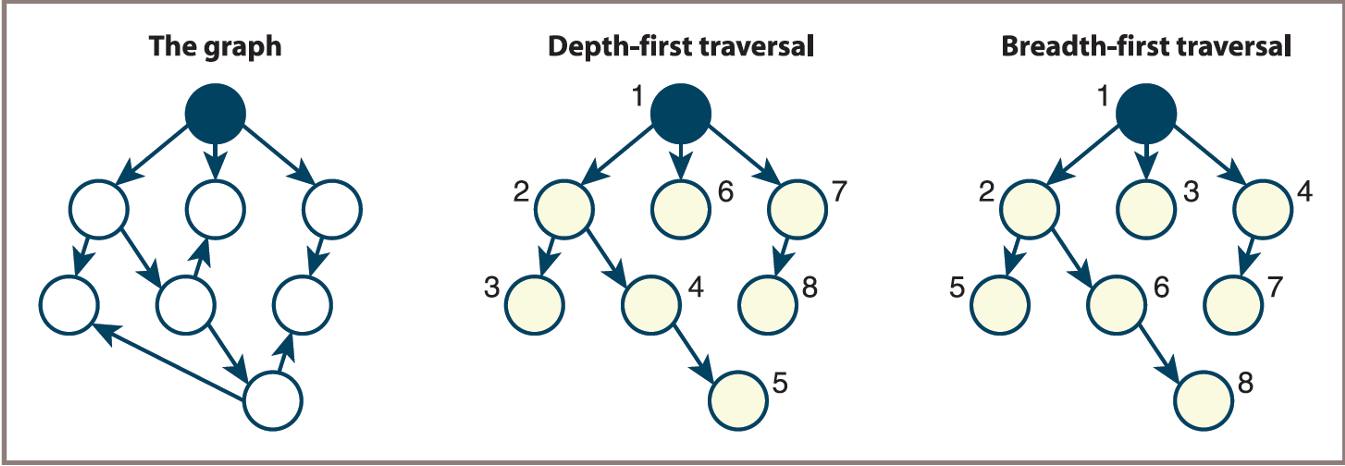
- Depth-first traversal – uses a stack as the collection in the generic algorithm
- Breadth-first traversal – uses a queue as the collection in the generic algorithm
The use of a stack forces the traversal process to go deeply into the graph before backtracking to another path
The use of a queue forces the traversal process to visit every vertex adjacent to a given vertex before it moves deeper into the graph

Common Order of Graph Traversals

Depth-First Traversal (DFS):
- Explores as far as possible along each branch before backtracking.
- Uses a stack (explicit or via recursion).
- Useful for pathfinding, cycle detection, and topological sorting.
Breadth-First Traversal (BFS):
- Explores all neighbors at the current depth before moving to the next level.
- Uses a queue.
- Useful for finding shortest paths in unweighted graphs and connectivity.
Topological Sort:
- Traverses a directed acyclic graph (DAG) to order vertices so that for every directed edge u → v, u comes before v.
- Used in scheduling and dependency resolution.

Common Order of Graph Traversals

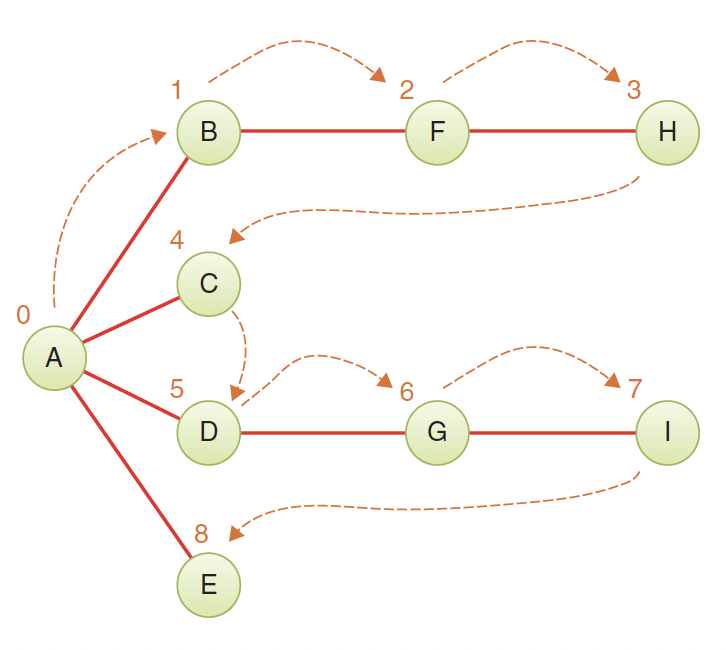
Depth-First Traversal (DFS):
This diagram shows the order in which the vertices are visited (which differ from the ID numbers used to identify vertices).

Common Order of Graph Traversals

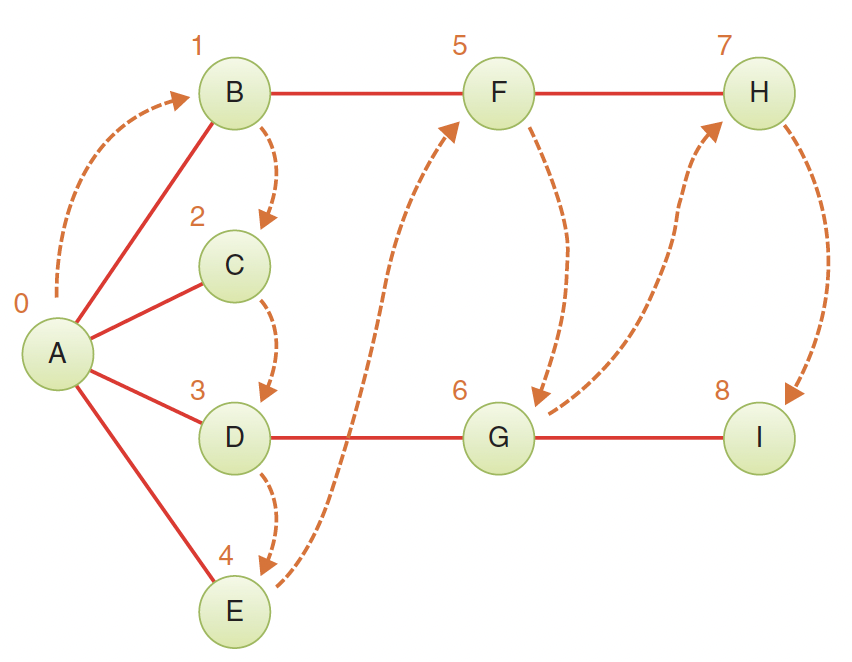
Breadth-First Traversal (BFS):
Here, you first visit A. Then you take all the vertices adjacent to A and insert each one into the queue as you visit and mark it.

DFS AND BFS Traversals

More Traversal Visualization here!

DFS and BFS Traversals

Psedocode: Iterative vs Recursive functions

traverseAll(graph, process):
    mark all vertices in the graph as unvisited
    instantiate an empty collection
    for each vertex in the graph:
        if the vertex has not been visited:
            add the vertex to the collection
        while the collection is not empty:
            pop a vertex from the collection
            if the vertex has not been visited:
                mark the vertex as visited
                process(vertex)
                add all adjacent unvisited vertices to the collection

DFS and BFS Traversals

Psedocode: Iterative vs Recursive functions

traverseAll(graph, process):
    mark all vertices in the graph as unvisited
    for each vertex, v, in the graph:
        if v is unvisited:
            dfs(graph, v, process)
     
dfs(graph, v, process):
    mark v as visited
    process(v)
    for each vertex, w, adjacent to v:
        if w is unvisited
            dfs(graph, w, process)

Graph Components

A graph component is a maximal connected subgraph, meaning every vertex in the component is reachable from every other vertex in that component, and no additional vertices from the graph can be included without losing connectivity.
In an undirected graph, components are simply called “connected components.”
In a directed graph, “strongly connected components” are subgraphs where every vertex is reachable from every other vertex via directed paths.
Identifying components helps analyze isolated clusters, connectivity, and structure within a graph.
You can use the traversal algorithms that have been discussed to partition the vertices of a graph into disjointed components.
- Here, each component could be stored in a set and sets are stored in a list:
  - Example: components = [{A, B, C}, {D, E}, {F}]

Trees within Graphs

The function traverseFromVertex shown in the Psedocode implicitly yields a tree rooted at the vertex from which the traversal starts and includes all the vertices reached during the traversal
Suppose dfs has just been called using vertex v:
- If a recursive call using vertex w now occurs, you can consider w to be a child of v The edge ( v , w ) corresponds to the parent-child relationship, or edge, between v and w
- The starting vertex is the root of this tree
- The tree is called a depth-first search tree

Spanning Trees

A spanning tree of a connected, undirected graph is a subgraph that includes all the vertices of the graph and is a tree (i.e., connected and acyclic).
Every connected graph has at least one spanning tree.
Spanning trees are useful for minimizing the number of edges while maintaining connectivity.
Minimum Spanning Tree (MST):
- A spanning tree with the smallest possible total edge weight.
- Common algorithms for finding MSTs include Kruskal’s and Prim’s algorithms.
Applications include network design, clustering, and approximation algorithms.

Minimum Spanning Tree

A Minimum Spanning Tree (MST) is a spanning tree of a weighted, connected, undirected graph with the smallest possible total edge weight.
MSTs are used in network design, clustering, and other optimization problems.
Kruskal’s Algorithm:
- Sort all edges by weight.
- Add edges one by one to the tree, skipping those that would form a cycle, until all vertices are connected.
Prim’s Algorithm:
- Start from any vertex.
- Grow the tree by repeatedly adding the smallest edge that connects a vertex in the tree to a vertex outside.
Both algorithms run in \(O(E \log V)\) time, where \(E\) is the number of edges and \(V\) is the number of vertices.

Minimum Spanning Tree

Robert C. Prim’s algorithm for finding a minimum spanning tree

minimumSpanningTree(graph):
    mark all vertices and edges as unvisited
    mark some vertex, say v, as visited
    for all the vertices:
        find the least weight edge from a visited vertex to an
        unvisited vertex, say w
        mark the edge and w as visited

Topological Sort

A topological sort of a directed acyclic graph (DAG) is a linear ordering of its vertices such that for every directed edge u → v, vertex u comes before v in the ordering.
Topological sorting is useful for scheduling tasks, resolving dependencies, and organizing data with precedence constraints.
Example Scenario:
- Imagine a university course catalog where each course may have prerequisites.
- Each course is a vertex, and a directed edge from course A to course B means “A is a prerequisite for B.”
- For example:
  - Math 101 → Math 201 (Math 101 is a prerequisite for Math 201)
  - CS 101 → CS 201 (CS 101 is a prerequisite for CS 201)
  - CS 201 → CS 301
  - Math 201 → CS 301
Only DAGs have valid topological orders; graphs with cycles do not.

Topological Sort

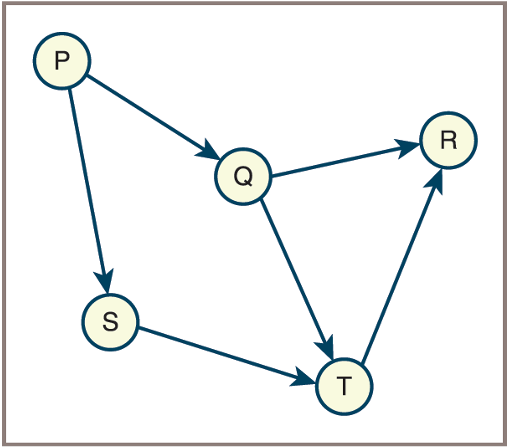
The first topological ordering of the graph
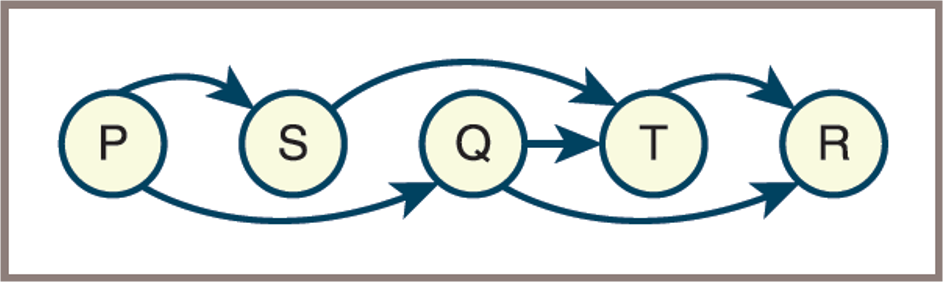
The first topological ordering of the graph

Class Worksheet Activity: 2

Event	Stack Contents
Visit A	A
Visit B	AB
Visit F	ABF
Visit H	ABFH
Pop H	ABF
Pop F	AB
Pop B	A
Visit C	AC
Pop C	A
Visit D	AD
Visit G	ADG
Visit I	ADGI
Pop I	ADG
Pop G	AD
Pop D	A
Visit E	AE
Pop E	A
Pop A
Done