TREES STRUCTURE (2)

Fred Agbo

2025-11-03

Announcements

• Welcome to New Month and week 11!
• We continue to discuss Trees Structure
  • Readings:
    • FDS - Lambert: Chapter 10
    • DS&A - John et al.: Chapter 8, 9
• Problem set 4 is due today at 10pm

Common Applications of Binary Trees

Common Applications of Binary Trees

• Heaps: Specialized binary trees used to implement priority queues.

• Binary Search Trees (BST): Efficiently support dynamic set operations such as search, insert, and delete.

• Expression Trees: Used to represent arithmetic expressions, where leaves are operands and internal nodes are operators.

• Huffman Coding Trees: Used in data compression algorithms to generate prefix codes.

• Syntax Trees: Used in compilers to represent the structure of program code.

• File System Indexing: Some file systems use binary trees for efficient file lookup.

• Routing Tables: Used in networking for efficient IP routing and searching.

• We will discuss the first three

Heaps

• A heap is a specialized binary tree-based data structure that satisfies the heap property:
  • In a max-heap, for every node, the value of the node is greater than or equal to the values of its children.
  • In a min-heap, for every node, the value of the node is less than or equal to the values of its children.
• Heaps are commonly implemented as complete binary trees, meaning all levels are fully filled except possibly the last, which is filled from left to right.

Types of Heaps

1. Min-Heap
   • The smallest element is at the root.
   • Every parent node has a value less than or equal to its children.
   • Used for priority queues where minimum element removal is required (e.g., Dijkstra’s algorithm).
2. Max-Heap
   • The largest element is at the root.
   • Every parent node has a value greater than or equal to its children.
   • Used in algorithms like Heap Sort and for implementing priority queues where maximum element removal is required.

• Either constraint on the order of the nodes is called the heap property

3. Other Heap Variants
   • d-ary Heap: Each node has d children instead of 2 (binary).
   • Fibonacci Heap: Supports faster amortized operations for some algorithms.
   • Binomial Heap: Used in parallel computing and supports efficient merging of heaps.

Heap Operations

• Insertion: Add the new element at the end (maintaining completeness), then “heapify up” to restore the heap property.
• Deletion (usually root): Remove the root, replace it with the last element, then “heapify down” to restore the heap property.
• Peek: Access the root element (max or min) in constant time.

Applications of Heaps

• Implementing priority queues
• Heap sort algorithm
  • Algorithm that builds a heap from a set of data and then repeatedly removes the root item and adds it to the end of a list
• Graph algorithms (e.g., Dijkstra’s shortest path)
• Order statistics (finding kth largest/smallest element)

Examples of Heaps

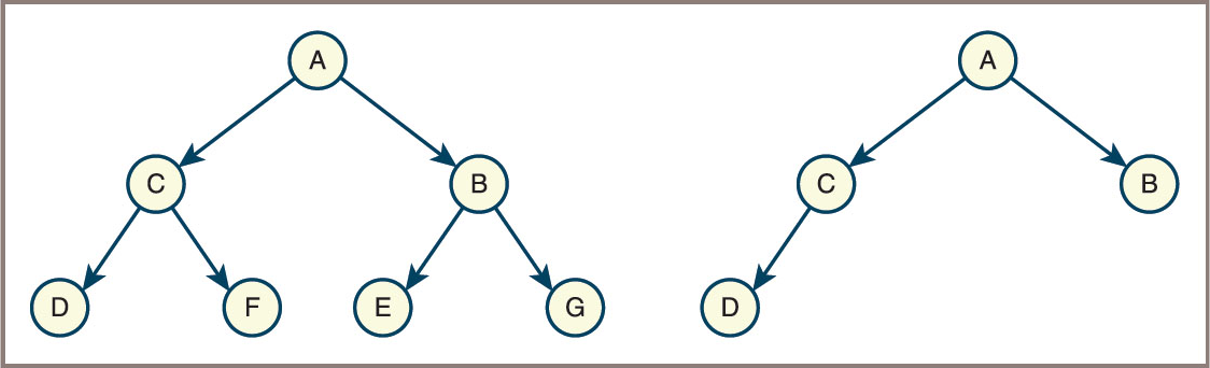
• Examples of a min-heap
• Draw the diagram to showcase an example of maz-heap
  • following the contraint on the order of its nodes

Binary Search Trees (BST)

• A Binary Search Tree (BST) is a binary tree in which each node has a key, and:
  • The key in each node is greater than all keys in its left subtree.
  • The key in each node is less than all keys in its right subtree.
• Key in this case is the value used for ordering
  • It can be the data stored itself (if simple values such as integer) or attribute/reference key used for comparison
• BSTs efficiently support dynamic set operations:
  • Search: Find if a value exists in O(h) time, where h is the height of the tree.
  • Insert: Add a new value while maintaining the BST property.
  • Delete: Remove a value and restructure the tree if necessary.

BST Example

• The possible search paths for the binary search of a sorted list

BST Example

• Binary Search Tree

BST Interface

• A binary search tree imposes a special ordering on the nodes in a binary tree
  • So it supports logarithmic searches and insertions
• The interface for a BST should include a constructor and the basic operations common to all collections
  • isEmpty , len , str , +, == , in , add , and count
• As with bags
  • Insertions and removals are accomplished by the add and remove methods
• The method __contains__
  • Performs a binary search in any BST implementation

BST Interface

• To allow users to retrieve and replace items in a binary search tree, the methods find and replace are also included.
  • The method find expects an item as an argument and returns the item matching it in the tree, or None otherwise
  • The method replace expects two items as arguments
• Because there are four ways to traverse a binary tree
  • You include methods for each one
• Each traversal method returns an iterator
  • The tree’s __iter__ method supports a preorder traversal
• Two trees are considered equal if they contain the same items in the same positions
• The str operation returns a string that shows the shape of the tree when printed.

BST Interface (Part 1)

Method	What It Does
tree.isEmpty()	Returns True if tree is empty, False otherwise.
tree.__len__()	Same as len(tree). Returns the number of items in the tree.
tree.__str__()	Same as str(tree). Returns a string showing the shape of the tree when printed.
tree.__iter__()	Same as iter(tree) or for item in tree:. Performs a preorder traversal on the tree.
tree.__contains__(item)	Same as item in tree. Returns True if item is in the tree, False otherwise.
tree.__add__(otherTree)	Same as tree + otherTree. Returns a new tree containing items from both trees.
tree.__eq__(anyObject)	Same as tree == anyObject. Returns True if trees are equal (same items in corresponding positions).

BST Interface (Part 2)

Method	What It Does
tree.clear()	Makes the tree become empty.
tree.add(item)	Adds item to its proper place in the tree.
tree.remove(item)	Removes item from the tree. Precondition: item is in the tree.
tree.find(item)	Returns the matched item if found, otherwise returns None.
tree.replace(item, newItem)	Replaces matched item with newItem and returns the matched item, else returns None.
tree.preorder()	Returns an iterator for preorder traversal.
tree.inorder()	Returns an iterator for inorder traversal.
tree.postorder()	Returns an iterator for postorder traversal.
tree.levelorder()	Returns an iterator for level order traversal.

Steps for Implementing Linked-Based BST

Implementing a Linked-Based BST

Step 1: Define the BSTNode Class

• Represents a single node in the BST.
• Contains fields for the data, left child, and right child.

Step 1: Define the BSTNode Class

"""file: bstnode.py"""
class BSTNode:
        """Represents a node for a linked binary search tree."""
        def __init__(self, data, left=None, right=None):
            self.data = data
            self.left = left
            self.right = right

Implementing a Linked-Based BST

Step 2: Create the BSTInterface

• Specifies the required methods for any BST implementation (e.g., add, remove, find, traversal methods).
• Can be defined as an abstract base class.

Step 2: Create the BSTInterface

"""
File: BSTinterface.py
Author: Ken Lambert
"""
class BSTInterface(object):
    """Interface for all binary search trees."""

    # Constructor
    def __init__(self, sourceCollection = None):
        """Sets the initial state of self, which includes the
        contents of sourceCollection, if it's present."""
        pass

    # Accessor methods
    def isEmpty(self):
        """Returns True if len(self) == 0, or False otherwise."""
        return True
    
    def __len__(self):
        """-Returns the number of items in self."""
        return 0

    def __str__(self):
        """Returns the string representation of self."""
        return ""

    def __iter__(self):
        """Supports a preorder traversal on a view of self."""
        return None

    def inorder(self):
        """Supports an inorder traversal on a view of self."""
       return None

    def postorder(self):
        """Supports a postorder traversal on a view of self."""
        return None

    def levelorder(self):
        """Supports a levelorder traversal on a view of self."""
        return None

    def __add__(self, other):
        """Returns a new bag containing the contents
        of self and other."""
        return None

    def __eq__(self, other):
        """Returns True if self equals other,
        or False otherwise."""
        return False

    def __contains__(self, item):
        """Returns Ture if item is in self, or
        False otherwise."""
        return True

    def find(self, item):
        """If item matches an item in self, returns the
        matched item, or None otherwise."""
        return None

    # Mutator methods
    def clear(self):
        """Makes self become empty."""
        pass

    def add(self, item):
        """Adds item to self."""
        pass

    def remove(self, item):
        """Precondition: item is in self.
        Raises: KeyError if item is not in self.
        postcondition: item is removed from self."""
        pass

    def replace(self, item, newItem):
        """Precondition: item == newItem.
        Raises: KeyError if item != newItem.
        If item is in self, replaces it with newItem and
        returns the old item, or returns None otherwise."""
        return None

Implementing a Linked-Based BST

Step 3: Implement AbstractCollection

• Provides basic collection behaviors (e.g., isEmpty, __len__, clear).

Step 3: Implement AbstractCollection

"""
File: abstractcollection.py
Author: Ken Lambert
"""
class AbstractCollection(object):
    """An abstract collection implementation."""

    # Constructor
    def __init__(self, sourceCollection = None):
        """Sets the initial state of self, which includes the
        contents of sourceCollection, if it's present."""
        self.size = 0
        if sourceCollection:
            for item in sourceCollection:
                self.add(item)

    # Accessor methods
    def isEmpty(self):
        """Returns True if len(self) == 0, or False otherwise."""
        return len(self) == 0
    
    def __len__(self):
        """Returns the number of items in self."""
        return self.size

    def __str__(self):
        """Returns the string representation of self."""
        return "[" + ", ".join(map(str, self)) + "]"

    def __add__(self, other):
        """Returns a new bag containing the contents
        of self and other."""
        result = type(self)(self)
        for item in other:
            result.add(item)
        return result

    def __eq__(self, other):
        """Returns True if self equals other,
        or False otherwise."""
        if self is other: return True
        if type(self) != type(other) or \
           len(self) != len(other):
            return False
        otherIter = iter(other)
        for item in self:
            if item != next(otherIter):
                return False
        return True

    def count(self, item):
        """Returns the number of instances of item in self."""
        total = 0
        for nextItem in self:
            if nextItem == item:
                total += 1
        return total

Implementing a Linked-Based BST

Step 4: Implement the LinkedBST Class

• Inherit from BSTInterface and AbstractCollection.
• Use BSTNode for the tree structure.
• Implement all required BST operations (add, remove, find, traversals, etc.).

Step 4: Implement the LinkedBST Class

"""
File: linkedbst.py
Author: Ken Lambert
"""
from abstractcollection import AbstractCollection
from bstnode import BSTNode

class LinkedBST (AbstractCollection):
    """An link-based binary search tree implementation."""

    def __init__(self, sourceCollection = None):
        """Sets the initial state of self, which includes the
        contents of sourceCollection, if it's present."""
        self.root = None
        AbstractCollection.__init__(self, sourceCollection)

        # Implement add, remove, find, __contains__, __iter__, etc.

Implementing a Linked-Based BST

Step 5 & 6:

• Implement Traversal Methods
  • Preorder, inorder, postorder, and level order traversals as generator methods.
• Test the Implementation
  • Create instances, add/remove/find items, and verify traversals.

Searching a Binary Search Tree

• The find method returns the first matching item if the target item is in the tree
• Otherwise, it returns None
• Pseudocode algorithm for this process:

if the tree is empty
    return None
else if the target item equals the root item
    return the root item
else if the target item is less than the root item
    return the result of searching the left subtree
else
    return the result of searching the right subtree

Traversing a Binary Search Tree

• General recursive strategy for an inorder traversal of a binary tree:

if the tree is not empty
    visit the left subtree
    visit the item at the root of the tree
    visit the right subtree

• Code for the recursive implementation of the inorder method:

def inorder(self):
    """Supports an inorder traversal on a view of self."""
    lyst = list()
 
    def recurse(node):
        if node != None:
            recurse(node.left)
            lyst.append(node.data)
            recurse(node.right)
 
    recurse(self.root)
    return iter(lyst)

The String Representation of BST

• Code that builds the appropriate string by first recusing with the right subtree, then visiting an item, and finally recursing with the left subtree:

def __str__(self):
    """Returns a string representation with the tree rotated
    90 degrees counterclockwise."""
    def recurse(node, level):
        s = ""
        if node != None:
            s += recurse(node.right, level + 1)
            s += "| " * level
            s += str(node.data) + "\n"
            s += recurse(node.left, level + 1)
        return s
    return recurse(self.root, 0)

Inserting an Item into BST

• The add method inserts an item into its proper place in the binary search tree
• An item’s proper place will be in one of three positions:
  • The root node, if the tree is already empty
  • A node in the current node’s left subtree, if the new item is less than the item in the current node
  • A node in the current node’s right subtree, if the new item is greater than or equal to the item in the current node
• For the second and third options, the add method uses a recursive helper function named recurse

Inserting an Item into BST

• Code for the add method:

def add(self, item):
    """Adds item to the tree."""
 
    # Helper function to search for item’s position
    def recurse(node):
        # New item is less; go left until spot is found
        if item < node.data:
            if node.left == None:
                node.left = BSTNode(item)
            else:
                recurse(node.left)
        # New item is greater or equal;
        # go right until spot is found
        elif node.right == None:
            node.right = BSTNode(item)
        else:
            recurse(node.right)
        # End of recurse
 
    # Tree is empty, so new item goes at the root
    if self.isEmpty():
        self.root = BSTNode(item)
    # Otherwise, search for the item’s spot
    else:
        recurse(self.root)
    self.size += 1

Removing an Item from a BST

• Save a reference to the root node
• Locate the node to be removed, its parent, and its parent’s reference to this node
• If the node has a left child and a right child, replace the node’s value with the largest value in the left subtree and delete that value’s node from the left subtree
• Otherwise, set the parent’s reference to the node to the node’s only child
• Reset the root node to the saved reference
• Decrement the size and return the item

Complexity Analysis of BST

• Optimal behavior depends on the height of the tree
• Run time of insertions is also highly dependent on the height of the tree
  • Removals also require a search for the target item
• Strategies for maintaining a tree structure that supports optimal insertions and searches in all cases
  • Are the subject of advanced computer science courses